A Leonardo Eulero (1707-1783), di cui quest’anno ricorre centenario della nascita, si deve il seguente problema:
«Tre gentiluomini giocano insieme: nella prima partita il primo perde, a favore degli altri due, tanto denaro quanto ne possiede ciascuno di loro.
Nella successiva, il secondo gentiluomo perde a favore di ciascuno degli altri due tanto denaro quanto essi già ne possiedono.
Da ultimo, nella terza partita, il primo e il secondo guadagnano ciascuno dal terzo gentiluomo tanto denaro quanto ne avevano prima.
A questo punto smettono e trovano che ciascuno ha la stessa somma, cioè 24 luigi.
Si domanda con quanto denaro si sedette a giocare».
Osserva
| Valori iniziali | x | y | z |
| Dopo la 1° partita | x-y-z | y+y 2y | z+z 2z |
| Dopo la 2° partita | (x-y-z)+(x-y-z) 2x-2y-2z | 2y-(x-y-z)-2z -x+3y-z | 2z+2z 4z |
| Dopo la 3° partita | (2x-2y-2z)+(2x-2y-2z) 4x-4y-4z | (-x+3y-z)+(-x+3y-z) -2x+6y-2z | 4z-(2x-2y-2z)-(-x+3y-z) -x-y+7z |
Si ottiene il sistema
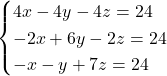
con la soluzione