Si scelga a caso un punto P all’interno di un cerchio.
Si determini la probabilità che esso sia più vicino al centro che alla circonferenza del cerchio.
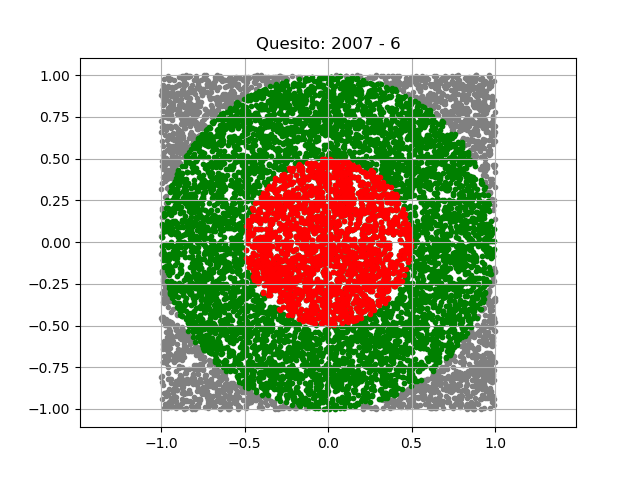
Immagine provvisoria realizzata con matplotlib
Osserva
- r : raggio
- d : distanza di P dal centro
- D: distanza di P dalla circonferenza
- d + D = r
Un punto è più vicino al centro che alla circonferenza del cerchio se
- d < D
- d < r – d
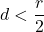
La probabilità che un punto del cerchio appartenga al cerchio interno è data dal rapporto tra le aree dei due cerchi
![]() =
= ![]() =
= 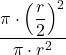 = … =
= … = ![]() = 0,25 = 25 %
= 0,25 = 25 %