Tenuto conto che ![]() si calcoli un’approssimazione di π, utilizzando uno dei metodi d’integrazione numerica studiati.
si calcoli un’approssimazione di π, utilizzando uno dei metodi d’integrazione numerica studiati.
Metodo dei trapezi
| n | h | i | xi | yi | Area | = |
| 1 | 0 | = 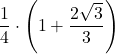 | ||||
| 1 | = | |||||
| Pi greco | = | |||||
= 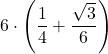 | ||||||
| = | ||||||
| = 3,232051 | ||||||
| n | h | i | xi | yi | Area | = |
| 2 | 0 | = 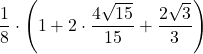 | ||||
| 1 | = | |||||
| 2 | Pi greco | = | ||||
= 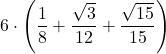 | ||||||
| = | ||||||
| = 3,165219 | ||||||
| n | h | i | xi | yi | Area | = |
| 3 | 0 | = 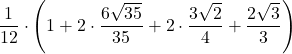 | ||||
| 1 | = | |||||
| 2 | Pi greco | = | ||||
| 3 | = 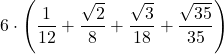 | |||||
| = | ||||||
| = 3,152196 | ||||||
| n | h | i | xi | yi | Area | = |
| 4 | 0 | = 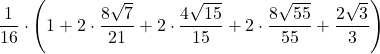 | ||||
| 1 | = | |||||
| 2 | Pi greco | = | ||||
| 3 | = 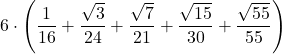 | |||||
| 4 | = | |||||
| = 3,147578 |