Esame di Stato 2013 PNI – 5

In un libro si legge: “se per la dilatazione corrispondente a un certo aumento della temperatura un corpo si allunga (in tutte le direzioni) di una certa percentuale (per es. 0,38%), esso si accresce in volume in proporzione tripla (cioè dell’1,14%) mentre la sua superficie si accresce in proporzione doppia (cioè del 0,76%)”.

È così? Si motivi esaurientemente la risposta.

Un aumento del 0,38% per le 3 dimensioni

$\displaystyle x_2 = x_1+\frac{0,38}{100}\cdot x_1 = 1,0038 \cdot x_1$

$\displaystyle y_2 = y_1+\frac{0,38}{100}\cdot y_1 = 1,0038 \cdot y_1$

$\displaystyle z_2 = z_1+\frac{0,38}{100}\cdot z_1 = 1,0038 \cdot z_1$

comporta per il volume

$\displaystyle V_2 = (1,0038 \cdot x_1)(1,0038 \cdot y_1)(1,0038 \cdot z_1) = (1,0038)^3 \cdot V_1 = (1,0114...)\cdot V_1$ (+1,14 %)

e per la superficie

$\displaystyle S_2 = \dots = (1,0038)^2 \cdot S_1 = (1,0076...)\cdot S_1$ (+0,76 %)

Approfondimento 1

All’aumentare della dimensione come aumenta la superficie?
Sia x=100

$\Delta x$	$x+\Delta x$	$\left (x+\Delta x\right)^2$	$x^2+2 x \Delta x + (\Delta x)^2$	$\displaystyle x^2 \left(1+2 \left(\frac{ \Delta x}{x}\right) + \left(\frac{ \Delta x}{x}\right)^2\right)$
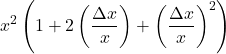0,1	100,1	10.020,01 (+0,2001%)	10.000 +20 +0,01	10.0001 10.0000,002 10.000*0,000001
1,0	101,0	10.201,00 (+2,01%)	10.000 +200 +1	10.0001 10.0000,02 10.000*0,0001
10	110,0	12.100,00 (+21,0%)	10.000 +2.000 +100	10.0001 10.0000,2 10.000*0,01

Approfondimento 2

All’aumentare della dimensione come aumenta il volume?
Sia x=100

$\Delta x$	$x+\Delta x$	$\left (x+\Delta x\right)^3$	$x^3+3 x^2 \Delta x + 3 x (\Delta x)^2 + (\Delta x)^3$	$\displaystyle x^3 \left(1+3 \left(\frac{ \Delta x}{x}\right) + 3 \left(\frac{ \Delta x}{x}\right)^2 + \left(\frac{ \Delta x}{x}\right)^3 \right)$
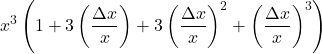0,1	100,1	1.003.003,001 (+0,3003001%)	1.000.000 +3.000 +3 +0,001	1.000.0001 1.000.0000,003 1.000.000*0,000003 1.000.000*0,000000001
1,0	101,0	1.030.301 (+3,0301%)	1.000.000 +30.000 +300 +1	1.000.0001 1.000.0000,03 1.000.000*0,0003 1.000.000*0,000001
10	110,0	1.331.000 (+33,1%)	1.000.000 +300.000 +30.000 +1.000	1.000.0001 1.000.0000,3 1.000.000*0,03 1.000.000*0,001