Esame di Stato 2014 PNI – 3

di

Venti palline sono poste in un’urna.
Cinque sono rosse, cinque verdi, cinque gialle e cinque bianche.
Dall’urna si estraggono a caso, senza reimbussolamento, tre palline.

Si valutino le seguenti probabilità:

  1. esattamente una pallina è rossa;
  2. le tre palline sono di colori differenti.

1. Esattamente una pallina è rossa

La prima rossa, la seconda e la terza non rossa

p() = p() · p( | ) · p( | ) = \displaystyle \frac{5}{20}\cdot\frac{15}{19}\cdot\frac{14}{18}

La prima non rossa, la seconda rossa e la terza non rossa

p() = p() · p( | ) · p( | ) = \displaystyle \frac{15}{20}\cdot\frac{5}{19}\cdot\frac{14}{18}

La prima e la seconda non rossa e la terza rossa

p() = p() · p( | ) · p( | ) = \displaystyle \frac{15}{20}\cdot\frac{14}{19}\cdot\frac{5}{18}

p(“una sola rossa”) = \displaystyle 3\cdot\frac{15}{20}\cdot\frac{14}{19}\cdot\frac{5}{18} = \displaystyle \frac{35}{76} = 46,05…%

2. Le tre palline sono di colori differenti

La prima di colore qualsiasi: 1

La seconda diversa dalla prima: \displaystyle \frac{15}{19}

La terza diversa da entrambe: \displaystyle \frac{10}{18}

p(“diverse”) = \displaystyle \frac{15}{19}\cdot \frac{10}{18} = \displaystyle \frac{25}{57} = 43,859…%

Soluzione 2

Calcola il numero di disposizioni

3 palline su 20: \displaystyle {20 \choose 3} = \displaystyle \frac{20!}{3!17!}

2 palline su 15: \displaystyle {15 \choose 2}} = \displaystyle \frac{15!}{2!13!}

1 pallina su 5: \displaystyle {5 \choose 1}

3 palline su 4: \displaystyle {4 \choose 3}

e poi le probabilità

Esattamente una pallina è rossa: 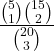\displaystyle \frac{{5 \choose 1}{15 \choose 2}}{{20 \choose 3}} = … = \displaystyle \frac{35}{76} = …

Le tre palline sono di colori differenti: 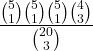\displaystyle \frac{{5 \choose 1}{5 \choose 1}{5 \choose 1}{4 \choose 3}}{{20 \choose 3}} = … = \displaystyle \frac{25}{57} = …