Il caso del barile

di


Sei il giudice che deve sentenziare in merito al seguente caso.

Filippo sta passeggiando nei pressi di un magazzino di proprietà di Giorgio, e viene colpito da un barile, riportando delle ferite.
Il barile era stato sollevato dal suolo e stava per essere riposto nel magazzino dai dipendenti di Giorgio.
Gli operai non si spiegano come sia potuto accadere che il barile sia caduto.

I casi sono due

  • il barile era stato fissato male (negligenza di un operaio)
  • oppure la corda era difettosa e si è spezzata.

Sai che

  • se un barile viene fissato male nel 90% dei casi cade
  • se il barile viene fissato bene si stacca solamente nell’1% dei casi
  • i lavoratori sono negligenti 1 volta su 1000

Quale sarebbe la tua sentenza?

  1. Gli operai hanno fissato male il barile e dunque Giorgio deve essere giudicato colpevole.
  2. La corda era difettosa e si è spezzata, quindi non si può ritenere Giorgio colpevole del fatto.
  3. Non so

Sia

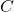  • C = “barile cade”
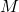  • M = “barile fissato male”
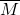  • \overline{M} = “barile fissato bene”

Osserva

Il barile cade,
era stato fissato male		\displaystyle p(C\ |\ M)= \displaystyle \frac{90}{100}= 0,9
Il barile cade,
era stato fissato bene		\displaystyle p(C\ |\ \overline{M})= \displaystyle \frac{1}{100}= 0,01
Il barile è stato fissato male\displaystyle p(M)= \displaystyle \frac{1}{1000}= 0,001
Il barile è stato fissato bene\displaystyle p(\overline{M})= \displaystyle \frac{999}{1000}= 0,999
Il barile cade\displaystyle p(C)= \displaystyle p(M)\cdot p(C\ |\ M) + p(\overline{M})\cdot p(C\ |\ \overline{M})
= \displaystyle \frac{1}{1000} \cdot \frac{90}{100} + \frac{999}{1000} \cdot \frac{1}{100} = \displaystyle \frac{90}{100.000} + \frac{999}{100.000} = \displaystyle \frac{1089}{100.000} = 0,01089
Il barile è stato fissato male,
sapendo che è caduto		\displaystyle p(M\ |\ C)= \displaystyle \frac{p(M)\cdot p(C\ |\ M)}{p(C)} = \displaystyle \frac{p(M)\cdot p(C\ |\ M)}{p(M)\cdot p(C\ |\ M) + p(\overline{M})\cdot p(C\ |\ \overline{M})}…
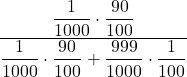= \displaystyle \frac{\displaystyle\frac{1}{1000} \cdot \frac{90}{100}}{\displaystyle\frac{1}{1000} \cdot \frac{90}{100} + \frac{999}{1000} \cdot \frac{1}{100}} = \displaystyle \frac{90}{1089}= 0,0826446…
Il barile è stato fissato bene,
sapendo che è caduto		\displaystyle p(\overline{M}\ |\ C)= \displaystyle \frac{p(\overline{M})\cdot p(C\ |\ \overline{M})}{p(C)} = \displaystyle \frac{p(\overline{M})\cdot p(C\ |\ \overline{M})}{p(M)\cdot p(C\ |\ M) + p(\overline{M})\cdot p(C\ |\ \overline{M})}
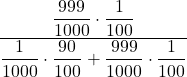= \displaystyle \frac{\displaystyle \frac{999}{1000} \cdot \frac{1}{100}}{\displaystyle \frac{1}{1000} \cdot \frac{90}{100} + \frac{999}{1000} \cdot \frac{1}{100}} = \displaystyle \frac{999}{1089}= 0,917355…

Quindi… sapendo che il barile è caduto la probabilità che la corda si sia è spezzata è ~92% mentre la probabilità che ci sia stata negligenza degli operai è ~8%