La confederazione IMO

Olimpiadi di Matematica – Gara Nazionale a Squadre 2001 – Numero 1

La confederazione IMO è una pacifica civiltà aliena che si trova nella Galassia Asip.
La galassia è formata da $n$ gruppi di stelle ciascuno dei quali forma un cerchio.
Il cerchio più piccolo (chiamato $I_1$ ) ha raggio $1$ Imoparsec.
Se ad esso si circoscrive un quadrato e a questo si circoscrive un cerchio si trova la seconda cintura di stelle $I_2$ .
In maniera analoga a partire da $I_3$ si ottiene $I_3$ e poi $I_4$ , $I_5$ , …
L’ultima cintura è l’unica che ha un raggio più grande di 2001 Imoparsec.
Quante sono in tutto le cinture?

Soluzione 1

Calcola i valori per i raggi al crescere dell’indice

1
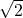$\sqrt{2}$ = 1,41421
2
$2\cdot\sqrt{2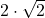}$ = 2,82843
4
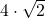$4\cdot\sqrt{2}$ = 5,65685
8
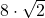$8\cdot\sqrt{2}$ = 11,3137
16
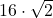$16\cdot\sqrt{2}$ = 22,6274
32
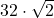$32\cdot\sqrt{2}$ = 45,2548
64
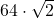$64\cdot\sqrt{2}$ = 90,5097
128
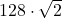$128\cdot\sqrt{2}$ = 181,019
256
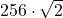$256\cdot\sqrt{2}$ = 362,039
512
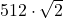$512\cdot\sqrt{2}$ = 724,077
1024
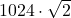$1024\cdot\sqrt{2}$ = 1448,15
2048

Soluzione 2

Al crescere dell’indice dispari il valore del raggio è
- $(2\cdot n+1) \rightarrow 2^n, n=0,1,...$
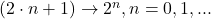
- Per
  - $(23) \rightarrow 2048$
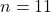
Al crescere dell’indice pari il valore del raggio è
- $(2\cdot n) \rightarrow 2^{n-1}\cdot \sqrt{2}, n=1,2,...$
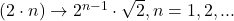
- Per
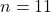
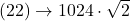  - $(22) \rightarrow 1024\cdot\sqrt{2}$ = 1448,15