Considera matrici quadrate di dimensione 2, 3, …

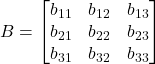
Matrice nulla
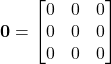
Proprietà
![]()
Matrice identità
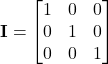
Proprietà
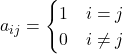
Matrici diagonali
Matrice diagonale principale
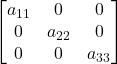
Proprietà
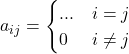
Matrice diagonale secondaria (antidiagonale)

Proprietà
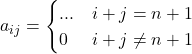
Matrici triangolari
Matrice triangolare superiore
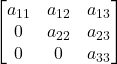
Proprietà
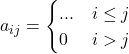
Matrice triangolare inferiore

Proprietà
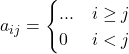
Trasposta
La trasposta di ![]() è la matrice con gli elementi “ribaltati” rispetto alla diagonale principale.
è la matrice con gli elementi “ribaltati” rispetto alla diagonale principale.
Le righe di ![]() diventano le colonne di
diventano le colonne di ![]() .
.
![]()
= 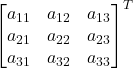
= 
Proprietà
Simmetrica
Una matrice A è simmetrica se è uguale alla sua trasposta
![]()
Proprietà
Prodotto per uno scalare
![]()
= 
= 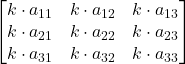
Proprietà
Addizione
![]()
![]()
= 
= 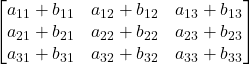
Proprietà
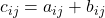
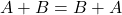
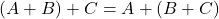
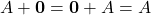
- La somma di due matrici triangolari (simili) è una matrice triangolare
- La somma di due matrici diagonali (simili) è una matrice diagonale
![]()
= 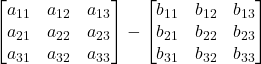
= 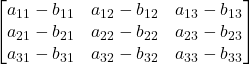
Proprietà
Prodotto
Se le due matrici non sono quadrate e della stessa dimensione allora sono compatibili per il prodotto se il numero di colonne di A è uguale al numero di righe di B
![]()
![]()
= 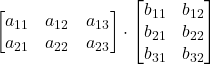
= ![]()
= ![]()
Proprietà
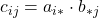
Prodotto scalare tra una riga di A e una colonna di B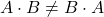
La moltiplicazione tra matrici non è commutativa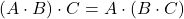
Se le matrici sono quadrate
![]()
![]()
= 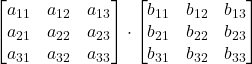
= 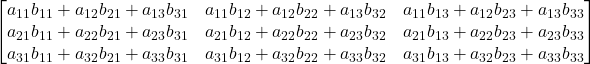
= 
Proprietà
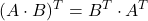
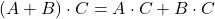
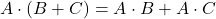
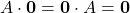
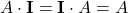
- Il prodotto di due matrici triangolari è una matrice triangolare
- Il prodotto di due matrici diagonali è una matrice diagonale