Proprietà del determinante

Il determinante della trasposta non cambia

$|A^T| = |A|$

Il determinante del prodotto è uguale al prodotto dei determinanti

$|A \cdot B| = |A| \cdot |B|$

La matrice identità ha determinante uguale a uno.

$|I| = 1$

Ancora

Il determinante della matrice diagonale (triangolare) è uguale al prodotto degli elementi della diagonale principale: $|A| = \prod_i a_{ii}$ .
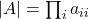Se si scambiano tra loro due righe il determinante cambia di segno.
Se si moltiplica una riga per una costante anche il determinante sarà moltiplicato per la costante.
Se a una riga viene sommato un multiplo di un’altra riga il determinante non cambia.
Una matrice è non singolare se il determinante non è nullo.

Calcolo del determinante