QUESITI sul Calcolo combinatorio

di

Esame
O.I.I.
Test

Anno 2001 – 6

Dimostrare che si ha \displaystyle {n \choose k} ={n-1 \choose k}+{n-1 \choose k-1} dove n, k sono numeri naturali qualsiasi, con n > k > 0.

Anno 2003 PNI – 1

Quante partite di calcio della serie A vengono disputate complessivamente (andata e ritorno) nel campionato italiano a 18 squadre?

SOLUZIONE 1

  • Ogni turno si giocano 9 partite (18/2)
  • Un girone si sviluppo su 17 turni (ognuna delle 18 squadre gioca con le altre 17)
  • Ci sono 2 gironi (andata e ritorno)
  • 9 · 17 · 2 = 306

SOLUZIONE 2

  • Date 18 oggetti tutti diversi (A, B, C, …, T) in quanti modi diversi si possono elencare 2 oggetti?
  • Numero di disposizioni semplici di 18 oggetti presi 2 alla volta?
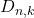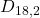    D_{n, k} = D_{18, 2} = 18 · 17 = 306
  • Numero di funzioni iniettive da un insieme di cardinalità 2 in uno di cardinalità 18?

Prova…

  • –, AB, AC, AD, …, AS, AT
  • BA, –, BC, BD, …, BS, BT
  • CA, CB, –, CD, …, CS, CT
  • …
  • TA, TB, TC, TD, …, TS, —

Osserva

  • La 1° scelta può essere una tra 18
  • La 2° scelta può essere una tra 17 (1 è stata già utilizzata)

Anno 2003 – 9

Si consideri una data estrazione in una determinata Ruota del Lotto.

Calcolare quante sono le possibili cinquine che contengono i numeri 1 e 90.

SOLUZIONE 1

  • (1, 2, 3, 4, 90), (1, 2, 3, 5, 90), …, (1, 2, 3, 89, 90) → 86
  • (1, 2, 4, 5, 90), …, (1, 2, 4, 89, 90) → 85
  • …
  • (1, 87, 88, 89, 90) → 1

Totale = ???

SOLUZIONE 2

Le possibili triple (x, y, z), ordinate, con valori diversi in 2…89 (88 valori) sono

\displaystyle {88 \choose 3} = \displaystyle \frac{88!}{3!(88-3)!} = \displaystyle \frac{88\cdot 87 \cdot 86}{3\cdot 2} = 109.736

Anno 2004 PNI – 4
Anno 2004 – 10

Dati gli insiemi A={1,2,3,4} e B={a,b,c} quante sono le applicazioni (le funzioni) di A in B?

Anno 2007 – 8

Si risolva l’equazione \displaystyle 4\ {n \choose 4} = 15\ {n-2 \choose 3}

Anno 2007 Suppletiva – 10

Si risolva la disequazione \displaystyle {x \choose 3} > \frac{15}{2}{x \choose 2}.

Anno 2007 Suppletiva PNI – 10

Si risolva la disequazione \displaystyle 5{x \choose 3} \le {x+2 \choose 3}.

Anno 2008 – 6

Se \displaystyle {n \choose 1}, \displaystyle {n \choose 2}, \displaystyle {n \choose 3}, con n>3, sono in progressione aritmetica, qual è il valore di n?

Anno 2009 – 7
Anno 2009 PNI – 7

Si dimostri l’identità \displaystyle {n \choose k+1} = {n \choose k}\ \frac{n-k}{k+1} dove n e k naturali e n > k.

Anno 2010 – 8

Se n>3 e \displaystyle {n \choose n-1}, \displaystyle {n \choose n-2}, \displaystyle {n \choose n-3}, sono in progressione aritmetica, qual è il valore di n?

Anno 2011 – 4
Anno 2011 PNI – 4

Il numero delle combinazioni di n oggetti a 4 a 4 è uguale al numero delle combinazioni degli stessi oggetti a 3 a 3.
Si trovi n.

Anno 2012 PNI – 5

Siano dati nello spazio n punti P1, P2, P3, …, PN.
Quanti sono i segmenti che li congiungono a due a due?
Quanti i triangoli che hanno per vertici questi punti (supposto che nessuna terna sia allineata)?
Quanti i tetraedri (supposta che nessuna quaterna sia complanare)?

OII 21-11-2001 – 4

Calcola in quanti diversi modi possiamo selezionare 3 diversi numeri dall’insieme {1, 2, 3, ..., 10} in modo tale che la somma dei tre numeri sia pari.
Ad esempio le terne {1,2,3} e {2,4,6} vanno bene mentre le terne {1,3,5} e {1,2,4} non vanno bene.
L’ordine di selezione non conta: ad esempio, {1,2,3} e {2,3,1} sono considerati la stessa terna.

OII 28-11-2001 – 3

In quanti modi possiamo distribuire 10 caramelle a 3 bambini Aldo, Beatrice e Carla, in modo tale che ogni bambino riceva almeno due caramelle?
Nota bene: le soluzioni (Aldo=3, Beatrice=3, Carla=4) e (Aldo=3, Beatrice=4, Carla=3) sono due soluzioni diverse.

OII 18-11-2004 – 2

Si consideri un torneo di calcetto in cui ogni squadra deve incontrare esattamente una volta tutte le altre.

Se il numero di partite del torneo è 136, quale è il numero delle squadre?

SOLUZIONE 1

Da (1, 2) a (1, n) sono n-1 partite
Da (2, 3 a (2, n) sono n-2 partite
…
Da (n-2, n-1) a (n-2, n) sono 2 partite
Ancora (n-1, n) è 1 partita

(n-1) + (n-2) + … + 2 + 1 = \displaystyle \frac{n\cdot (n-1)}{2} = 136

n=17

SOLUZIONE 2

In quanti modi si possono scegliere 2 squadre ordinate tra n squadre?

\displaystyle {n \choose 2} = 136

\displaystyle \frac{n\cdot (n-1)}{2} = 136

…

n=17

OII Allenamenti 2004 – 4

Biagio, l’allenatore della squadra di pallavolo di Vattelapesca, ha letto nel suo manuale del perfetto allenatore di pallavolo la seguente regola: in ogni momento in campo devono giocare un alzatore, due schiacciatori e tre universali.
Nella squadra sono disponibili complessivamente dieci giocatori, e, precisamente 2 alzatori, 3 schiacciatori, 5 universali.
Sapendo che un giocatore non può cambiare ruolo (ad esempio un alzatore non potrà giocare come schiacciatore o universale) quante diverse formazioni può schierare Biagio utilizzando i suoi dieci giocatori e rispettando la regola d’oro del suo manuale del perfetto allenatore.

Test 2012 – 72 ???

Determinare quante sono le parole di 7 lettere (anche senza senso) che si possono scrivere utilizzando solo le 4 lettere A, C, G, T (si intende che non bisogna necessariamente utilizzare tutte le 4 lettere, per cui per esempio anche la parola AGGTATA va bene).

  1. \displaystyle 4^7
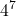
  2. (7 · 6 · 5 · 4) / (4 · 3 · 2)
  3. 7 · 6 · 5 · 4
  4. \displaystyle 7^4
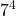
  5. 7 · 4

Test 2009 – 78

Tredici persone si stringono la mano. Ciascuna stringe la mano a tutte le altre. Quante sono le strette di mano in totale?

Quesiti di provenienza diversa, in ordine alfabetico…

…

A un concorso partecipano 15 candidati, e sono in palio 4 posti di lavoro identici.
In quanti modi possibili può essere formato il gruppo di vincitori?

…

Il piatto forte di “Gnam” sono gli hamburgher serviti con un’insalata ed una salsa.
I clienti possono comporre il loro piatto scegliendo tra 3 tipi di hamburgher, 4 diverse insalate e 2 salse.
Quanti piatti differenti si possono ricavare?

…

I numeri di telefono degli interni di una certa azienda sono composti da cinque cifre, di cui le prime tre sono 450.
Sapendo che le cifre dei numeri di telefono dell’azienda sono tutte diverse, qual è il numero massimo di numeri disponibili?

…

In una classe ci sono 20 alunni, di cui 16 giocano a calcio, 12 a pallacanestro e 11 a pallavolo.
Quanti sono al minimo, coloro che praticano tutti e tre gli sport?

…

In quanti modi si può formare una commissione di 3 uomini e 2 donne scelti tra 7 uomini e 2 donne?

…

Let be the set of natural numbers whose digits, in decimal representation, are chosen from {1,2,3} such that no digit is repeated.
Find the sum of all these numbers and put it in the box below.
Hint: note that, for example, the numbers 1, 12, 123 belong to.

…

Quante partite di calcio della serie A vengono disputate complessivamente (andata e ritorno) nel campionato italiano a 18 squadre?

…

Se ho un’enciclopedia formata da 10 libri, in quanti ordini possibili posso collocare i volumi?

…

Sette amici si siedono a una tavola, dove sono sistemate sette sedie.
In quanti modi diversi possono sedersi gli amici?

…

Stai cercando di decidere quale pizza vuoi ordinare per cena.
Rispetto alla base della pizza puoi scegliere fra: regolare, alta o sottile.
Rispetto al condimento puoi scegliere fra: margherita, margherita con l’aggiunta di un ingrediente o margherita con l’aggiunta di due ingredienti.
Fra quanti differenti tipi di pizza puoi scegliere?