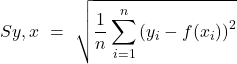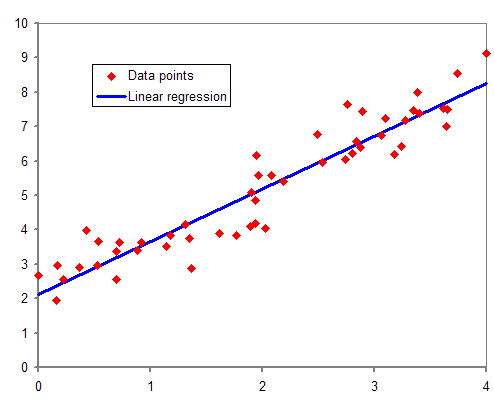
Considera un diagramma di dispersione (punti di coordinate x, y).
I punti descrivono grossolanamente una certa curva?
Tra le due variabili statistiche X e Y è possibile riconoscere una correlazione?
La regressione cerca la relazione esistente tra le due variabili.
- Curva di regressione
- Equazione di regressione:
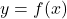
- Regressione lineare
- Regressione quadratica
- Regressione esponenziale
- Vedi Comandi Geogebra
Funzione interpolatrice lineare

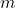 , coefficiente di regressione
, coefficiente di regressione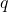 , costante di regressione
, costante di regressione
Interpolazione / Estrapolazione
Interpolazione: un’attività per individuare nuovi punti del piano cartesiano a partire da un insieme finito di punti dati.
Per valori della x che sono all’interno dell’intervallo dell’asse reale che contiene i punti nei quali sono noti i valori che essa assume.
Estrapolazione: un’attività per trovare valori di una funzione reale per valori della x che sono al di fuori dell’intervallo dell’asse reale che contiene i punti nei quali sono noti i valori che essa assume.
Errore, differenza tra l’ordinata di un punto e l’ordinata della funzione
![]()
Somma dei quadrati degli errori
![]()
= ![]()
= ![]()
Considerazioni matematiche…
Se le derivate parziali si annullano allora è presente un punto notevole (minimo)
![]() =
= ![]()
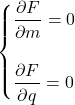
Calcoli…
![]()
![]()
![]()
![]()
![]()
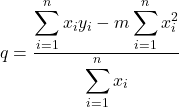
![]()
![]()
![]()
![]()
![]()

La soluzione del sistema è
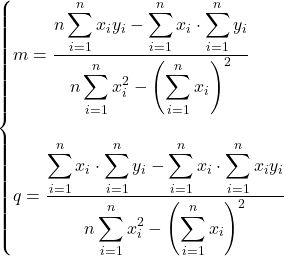
Formulazioni alternative
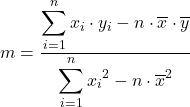
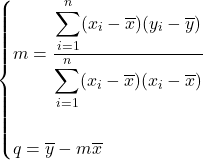
m = ![]()
Osservazione 1
La retta di regressione passa per il baricentro dei punti
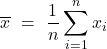 , media aritmetica
, media aritmetica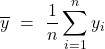 , media aritmetica
, media aritmetica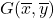 , baricentro dei punti
, baricentro dei punti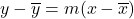
Osservazione 2
Dimostrazioni
![]()
=![]()
= ![]()
= ![]()
= ![]()
![]()
=![]()
= ![]()
= ![]()
= ![]()
Osservazione 3
m e ![]() hanno lo stesso segno
hanno lo stesso segno
Osservazione 4
Errore standard di stima: