 1
1
In una classe ci sono 20 alunni, di cui 16 giocano a calcio, 12 a pallacanestro e 11 a pallavolo.
Quanti sono al minimo, coloro che praticano tutti e tre gli sport?
2
Il prof. Verdi che dà lezioni private di matematica a cinque studenti, interrogherà i suoi studenti la settimana successiva; per esempio, se l’ordine estratto è BCAED significa che B verrà interrogato il lunedì, C il martedì e così via.
Per effettuare l’estrazione, il prof. Verdi usa un libro; su ciascuna pagina del libro il professore ha annotato uno degli ordini possibili; nessun ordine compare su più pagine, e ogni ordine possibile compare in qualche pagina.
Da quante pagine è composto il libro?
 3
3
In quanti modi possiamo distribuire 10 caramelle a 3 bambini Aldo, Beatrice e Carla, in modo tale che ogni bambino riceva almeno due caramelle?
Nota bene: le soluzioni
- Aldo=3 Beatrice=3 Carla=4
- Aldo=3 Beatrice=4 Carla=3
sono due soluzioni diverse.
4
Anna organizza il torneo di tennis del suo circolo; i partecipanti sono 200 e ad ogni incontro il perdente è eliminato dal torneo (nel tennis gli incontri non possono finire in parità).
Quante partite complessivamente saranno svolte per stabilire il vincitore?
- complessivamente si svolgono 100 partite
- complessivamente si svolgono 128 partite
- complessivamente si svolgono 199 partite
- complessivamente si svolgono 200 partite
- complessivamente si svolgono 255 partite
- dalle informazioni fornite non è possibile determinare esattamente il numero delle partite.
5
Il sig. Grassottelli si fa assegnare una dieta dal prof. Obesovitch.
La dieta prevede, fra l’altro, le seguenti restrizioni:
- ogni giorno si può mangiare pane o pasta, ma non entrambi;
- nell’arco di una giornata non si può mangiare sia formaggio che carne;
- se un certo giorno si mangia formaggio, non si può mangiare pasta;
- se un certo giorno si mangia pasta, non si può mangiare carne.
Considera le seguenti affermazioni
- non si può mai mangiare pasta
- non si possono mangiare formaggio e pasta lo stesso giorno
- se si mangia pasta, nello stesso giorno non si possono mangiare né carne né formaggio
- non si può mai mangiare carne
Quale delle seguenti possibilità è vera?
- L’affermazione A è vera e le altre sono false
- L’affermazione B è vera e le altre sono false
- L’affermazione C è vera e le altre sono false
- L’affermazione D è vera e le altre sono false
- Le affermazioni A e B sono vere e le altre sono false
- Le affermazioni A e C sono vere e le altre sono false
- Le affermazioni B e C sono vere e le altre sono false
- Le affermazioni C e D sono vere e le altre sono false.
6
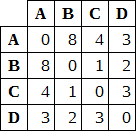
Sono date 4 città A, B, C, D e le distanze che le separano attraverso un collegamento diretto sono espresse dalla seguente matrice quadrata:
Ad esempio l’elemento di riga A e colonna B esprime il fatto che la distanza fra A e B utilizzando il collegamento diretto fra le città è pari a 8; analogamente si può verificare che la distanza del collegamento diretto fra D e C è pari a 3.
Ci chiediamo qual è la lunghezza complessiva del percorso più breve che partendo da A visita tutte le altre città senza passare nuovamente per A.
Ad esempio, se andiamo da A a B e poi da B a C e infine da C in D, la lunghezza complessiva del percorso è pari a 12 (infatti 8, 1 e 3 sono le distanze dei tre collegamenti).
Quale delle seguenti affermazioni è vera?
- la distanza del percorso più breve che partendo da A visita tutte le città, senza passare nuovamente per A, è pari a 6
- la distanza del percorso più breve che partendo da A visita tutte le città, senza passare nuovamente per A, è pari a 7
- la distanza del percorso più breve che partendo da A visita tutte le città, senza passare nuovamente per A, è pari a 8
- la distanza del percorso più breve che partendo da A visita tutte le città, senza passare nuovamente per A, è pari a 10
- la distanza del percorso più breve che partendo da A visita tutte le città, senza passare nuovamente per A, è pari a 12
- nessuna delle precedenti affermazioni fornisce correttamente la distanza del percorso più breve che partendo da A visita tutte le città senza passare nuovamente per A.