1
Bruno, il vincitore dell’ultima regata di Baia Baiella, si trova al bar con un gruppo di amici e parla della sua gara:
- Il percorso richiedeva di percorrere tre volte un triangolo equilatero.
- Visto che il vento non è variato durante tutta la regata, ho percorso i tre giri esattamente nella stessa maniera, ho cioè percorso ogni lato del percorso tre volte impiegando ogni volta lo stesso identico tempo.
- Per percorrere la prima metà del percorso ho impiegato 1 ora in più rispetto alla seconda metà per colpa del fatto che per percorrere il primo lato impiegavo 45 minuti in più rispetto al secondo lato.
Quale fra le seguenti frasi corrisponde al vero?
Risposte:
- per percorrere il terzo lato Bruno impiegava 5 minuti in meno rispetto al secondo lato
- per percorrere il terzo lato Bruno impiegava 10 minuti in meno rispetto al secondo lato
- per percorrere il terzo lato Bruno impiegava 15 minuti in meno rispetto al secondo lato
- nessuna delle precedenti frasi è vera.
2
Arturo ha in mano un mazzo di dieci carte numerate da 1 a 10.
Mescola le carte e le dispone una affiancata all’altra sul tavolo (ottenendo così una sequenza casuale delle carte). Arturo vuole ordinare in modo crescente le carte e per farlo deve effettuare degli scambi di posizione. Durante ogni scambio può scegliere 2 carte e scambiarle di posizione.
Se ad esempio le carte vengono disposte come segue: 1 2 5 7 3 6 4 8 9 10 sono sufficienti 2 scambi (5-3 e 7-4).
Arturo, prima di mettere le carte sul tavolo, vuole calcolare al massimo quanti scambi sarà costretto a fare (vuole cioè calcolare il numero minimo di scambi da farsi nel caso di peggiore disposizione delle carte).
Risposte:
- 5
- 9
- 10
- nessuna delle precedenti.
3 <–
Un ladro riesce ad aprire la cassaforte di una banca dove si trovano 100 sacchetti pieni d’oro, ma ha la possibilità di rubarne uno solo.
99 sacchetti hanno il medesimo contenuto mentre uno è più pesante in quanto contiene più oro. Chiaramente il ladro vuole portare con sé il sacchetto più pesante. Ha a disposizione una bilancia a due piatti: su ogni piatto può mettere la quantità di sacchetti che vuole, e la bilancia gli indica il piatto su cui è collocato il peso superiore. Prima di iniziare a pesare i sacchetti il ladro vuole calcolare quante pesate dovrà al massimo fare per avere la certezza di scegliere il sacchetto giusto.
Quante sono queste pesate?
Risposte:
- 6
- 7
- 99
- nessuna delle precedenti.
4
Supponiamo di avere di fronte a noi una scacchiera 8x8 e delle tessere del domino che hanno una dimensione tale da ricoprire esattamente 2 caselle adiacenti della scacchiera. Vogliamo coprire con le tessere tutta la scacchiera escluse due caselle collocate in due angoli opposti della scacchiera.
Dire quale delle seguenti frasi è vera:
- per ricoprire nel modo richiesto la scacchiera servono 32 tessere
- per ricoprire nel modo richiesto la scacchiera servono 31 tessere
- per ricoprire nel modo richiesto la scacchiera servono 30 tessere
- non è possibile riuscire a coprire la scacchiera nel modo richiesto.
5
Durante una serata particolarmente limpida, con un bel cielo stellato, Antonio si concentra a guardare una porzione di cielo in cui sono visibili esattamente 99 stelle. Antonio si chiede quale fra queste stelle sia la più vicina. Ha a disposizione uno speciale misuratore che ha la capacità di confrontare fra loro 3 stelle ed indicarne la più vicina.
Quale è il numero minimo di misurazioni che Antonio deve compiere per scoprire la stella più vicina?
Risposte:
- 33
- 49
- 99
- nessuna delle precedenti.
SOLUZIONE
Tratta da: Materiale didattico 2008
Numeriamo le stelle da 1 a 99 e subito cerchiamo il minimo tra le stelle 1, 2, 3.
Prendiamo il minimo e lo confrontiamo con le stelle 4, 5 e troviamo quindi il nuovo minimo.
Iteriamo quindi questo procedimento finché non arriviamo alle stelle 98 e 99.
All’inizio noi consideriamo le stelle 1, 2, 3 per cui da un totale di 99 stelle ne togliamo 3 e quindi abbiamo 96 stelle.
In ogni altro passaggio consideriamo invece il minimo precedente e aggiungiamo 2 stelle quindi al totale togliamo 2 stelle.
I passaggi saranno quindi1+(99-3)/2 = 49
.
6
Mario ha 24 anni ed ha il doppio dell’età che aveva Luisa quando lui aveva l’età che lei ha ora. Quanti anni ha Luisa?
Risposte:
- 16
- 20
- 18
- nessuna delle precedenti
7
Il medico ha consigliato a Mario di assumere una pillola tre volte al giorno, ad intervalli regolari, il tutto fino ad esaurire la confezione di 12 pillole. Se Mario inizia la cura in questo momento, fra quante ore l’avrà finita?
Risposte:
- 96
- 88
- 80
- nessuna delle precedenti.
8
Se tutti i belli sono ricchi e tutti i ricchi sono tristi, quale fra le seguenti frasi è corretta?
Risposte:
- alcuni tristi sono belli
- tutti i ricchi sono belli
- alcuni belli non sono tristi
- nessuna delle precedenti.
SOLUZIONE
Tratta da: Materiale didattico 2008
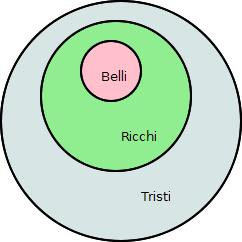
La situazione è rappresentabile con i tre insiemi Belli, Ricchi e Tristi (gli insiemi di verità delle tre proposizioni) uno incluso nell’altro:
Verifichiamo le affermazioni proposte:
- corretta, in quanto, se B non è vuoto, necessariamente degli elementi di T fanno anche parte di B.
- scorretta, perché è evidente che un elemento può appartenere ad R senza appartenere a B.
- scorretta, perché nel caso particolare in cui i tre insiemi B, R e T coincidono (situazione coerente con le premesse) allora tutti i belli sono necessariamente tristi.
- scorretta, essendo corretta a).
Osserva che
- Possono esistere ricchi che non sono belli
- Possono esistere tristi che non sono ricchi.
9
Se, a partire da due sequenze ordinate di n e m elementi, si deve ricostruire un’unica sequenza anch’essa ordinata …
Risposte:
- … si possono scandire tutti gli elementi delle due sequenze un’unica volta (cioè scandire n+m elementi)
- … si devono scandire tutti gli elementi della seconda sequenza per ogni elemento della prima sequenza (cioè scandire n*m elementi)
- … si devono scandire tutti gli elementi della prima sequenza e accodare quelli della seconda sequenza (cioè scandire n elementi)
- nessuna delle precedenti.
10
Sapendo che in un cubo di due metri di lato ci possono stare 8 cubi di un metro di lato, in una sfera di due metri di raggio quante sfere di un metro di raggio ci possono stare?
Risposte:
- 1
- 4
- 8
- nessuna delle precedenti.
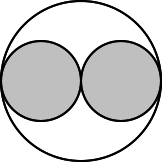
SOLUZIONE
Tratta da: Materiale didattico 2008
Osservare la figura relativa alla proiezione delle sfere sul piano
11
In quante parti al massimo si può suddividere una torta con quattro tagli?
Risposte:
- 8
- 11
- 14
- nessuna delle precedenti.
SOLUZIONE
Tratta da: Materiale didattico 2008
Il problema chiede in sostanza di contare in quante parti può essere partizionato al massimo lo spazio tagliandolo con n=4 piani.
L’idea, ad ogni nuovo taglio, è di intersecare tutti i piani precedenti.
Si osservi che
- per n=1 la risposta è 2,
- per n=2 la risposta è 4
- per n=3 la risposta è 8.
Tuttavia, per n=4, la risposta è 15.
La risposta generale a questa domanda, per n piani, è infatti data dalla formula:
C(n, 0) + C(n, 1) + C(n, 2) + C(n, 3)
dove con C(n, k) si è indica il numero delle combinazioni di n oggetti su k posti.
Nel nostro caso abbiamo quindi: 1+4+6+4 = 15.
La risposta esatta è quindi la d (nessuna delle precedenti).
La formula non è facilmente intuibile.
Si può trovare una spiegazione, ad esempio, in: Art of Counting.
12 <–
Una missione terrestre su Marte scopre una iscrizione. Sapendo che dopo lunghe analisi si interpreta che l’iscrizione riporti 5+4=11 quante dita per mano aveva il marziano (si assuma che il marziano abbia avuto due mani)?
Risposte:
- 4
- 5
- 6
- nessuna delle precedenti.