L’eliminazione di Gauss trasforma una matrice quadrata A in una matrice triangolare superiore T.
La matrice triangolare si presta al


A ogni passo si elimina (annulla) un elemento sotto la diagonale principale.
Alla sua riga si sottrae un certo multiplo di un’altra riga: ![]()

Eliminare ![]()
![]()
![]()
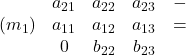
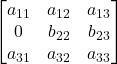
Eliminare ![]()
![]()
![]()
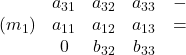
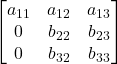
Eliminare ![]()
![]()
![]()
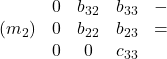
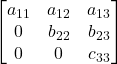
Matrice triangolare superiore
Eliminazione di Gauss-Jordan
Dopo essere arrivati alla matrice triangolare superiore si può continuare, dal basso verso l’alto, e ottenere una matrice diagonale.
La matrice diagonale si presta al


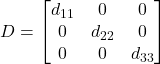
Esempio 2×2
![]()
Eliminare ![]()
![]()
![]() =
= ![]()
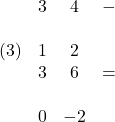
![]()
Eliminare ![]()
![]()
![]() =
= ![]()
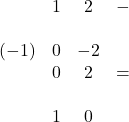
![]()
Matrice diagonale principale