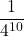Esame di Stato 2011 PNI – 7

di

Un test d’esame consta dieci domande, per ciascuna delle quali si deve scegliere l’unica risposta corretta fra quattro alternative.

Qual è la probabilità che, rispondendo a caso alle dieci domande, almeno due risultino corrette?

Osserva

  • Tutte errate: \displaystyle p_0=\left(\frac{3}{4}\right)^{10}
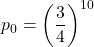
  • Una corretta (e 9 errate): \displaystyle p_1={10 \choose 1}\left(\frac{1}{4}\right)^{1}\left(\frac{3}{4}\right)^{9}
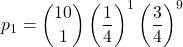
  • Almeno 2 corrette (tutti i risultati possibili tranne i due precedenti…):
    \displaystyle p_{\geq 2}=1-p_{0}-p_{1}
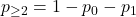
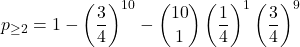    \displaystyle p_{\geq 2}=1-\left(\frac{3}{4}\right)^{10}-{10 \choose 1}\left(\frac{1}{4}\right)^{1}\left(\frac{3}{4}\right)^{9} = 0,7559… ~ 75,6%

Osserva le probabilità per numero di risposte corrette

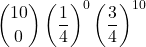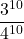
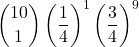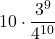
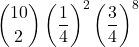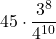
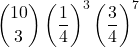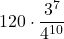
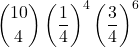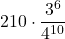
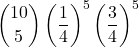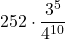
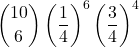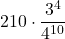
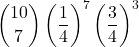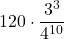
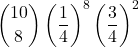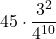
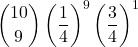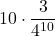
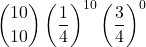  1. \displaystyle {10 \choose 0}\left(\frac{1}{4}\right)^{0}\left(\frac{3}{4}\right)^{10} = \displaystyle \frac{3^{10}}{4^{10}}
  2. \displaystyle {10 \choose 1}\left(\frac{1}{4}\right)^{1}\left(\frac{3}{4}\right)^{9} = \displaystyle 10\cdot\frac{3^{9}}{4^{10}}
  3. \displaystyle {10 \choose 2}\left(\frac{1}{4}\right)^{2}\left(\frac{3}{4}\right)^{8} = \displaystyle 45\cdot\frac{3^8}{4^{10}}
  4. \displaystyle {10 \choose 3}\left(\frac{1}{4}\right)^{3}\left(\frac{3}{4}\right)^{7} = \displaystyle 120\cdot\frac{3^7}{4^{10}}
  5. \displaystyle {10 \choose 4}\left(\frac{1}{4}\right)^{4}\left(\frac{3}{4}\right)^{6} = \displaystyle 210\cdot\frac{3^6}{4^{10}}
  6. \displaystyle {10 \choose 5}\left(\frac{1}{4}\right)^{5}\left(\frac{3}{4}\right)^{5} = \displaystyle 252\cdot\frac{3^5}{4^{10}}
  7. \displaystyle {10 \choose 6}\left(\frac{1}{4}\right)^{6}\left(\frac{3}{4}\right)^{4} = \displaystyle 210\cdot\frac{3^4}{4^{10}}
  8. \displaystyle {10 \choose 7}\left(\frac{1}{4}\right)^{7}\left(\frac{3}{4}\right)^{3} = \displaystyle 120\cdot\frac{3^3}{4^{10}}
  9. \displaystyle {10 \choose 8}\left(\frac{1}{4}\right)^{8}\left(\frac{3}{4}\right)^{2} = \displaystyle 45\cdot\frac{3^2}{4^{10}}
  10. \displaystyle {10 \choose 9}\left(\frac{1}{4}\right)^{9}\left(\frac{3}{4}\right)^{1} = \displaystyle 10\cdot\frac{3}{4^{10}}
  11. \displaystyle {10 \choose 10}\left(\frac{1}{4}\right)^{10}\left(\frac{3}{4}\right)^{0} = \displaystyle \frac{1}{4^{10}}