Esame di Stato 2009 – 8

19/05/202612/02/2017 di admin

Si provi che l’equazione $x^{2009}+2009x+1=0$ ha una radice compresa fra -1 e 0.

Studia gli zeri della funzione $f(x)=x^{2009}+2009x+1$

Esistenza

f(x) è continua in R
f(-1) = -2009
f(0) = +1
Segni discordi in [-1, 0]
Teorema degli zeri: esiste 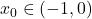$x_0 \in (-1, 0)$ tale che $f(x_0) = 0$ .

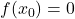Unicità

$f'(x)=2009x^{2008}+2009$
- $x^{2008}+1 = 0$
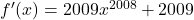
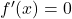
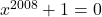
- impossibile
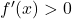$f'(x) > 0$ in R, f(x) crescente, no punti notevoli
Lo zero è unico

Conclusioni: l’equazione ha una e una sola soluzione reale, $x_0 \in (-1, 0)$ .

Approssimazione?

…