
Una pedina è collocata nella casella in basso a sinistra di una scacchiera, come in figura.
Ad ogni mossa, la pedina può essere spostata o nella casella alla sua destra o nella casella sopra di essa.
Scelto casualmente un percorso di 14 mosse che porti la pedina nella casella d’angolo opposta A, qual è la probabilità che essa passi per la casella indicata con B?
Soluzione 1
Il numero di percorsi per ogni coppia (partenza, arrivo) è dato dal numero di anagrammi diversi (permutazioni con ripetizioni) componibili con le lettere E (Est) e N (Nord)
Dalla partenza a A, 14 lettere, 7 lettere E, 7 lettere N
![]() = 3.432
= 3.432
Dalla partenza a B, 8 lettere, 3 lettere E, 5 lettere N
![]() = 56
= 56
Da B a A, 6 lettere, 4 lettere E, 2 lettere N
![]() = 15
= 15
Dalla partenza a A passando per B, 8 lettere, 3 lettere E, 5 lettere N, 6 lettere, 4 lettere E, 2 lettere N
![]() = 56·15 = 840
= 56·15 = 840
La probabilità di passare per B in un percorso dalla partenza a A
p = 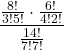 =
= ![]() = 0,244755… ~24,5%
= 0,244755… ~24,5%
Soluzione 2
Con gli stessi ragionamenti ma passando per i coefficienti binomiali
p = 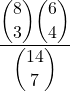 = …
= …
Soluzione 3
Compila le mappe scrivendo in ogni casella il numero di percorsi disponibili per raggiungerla, partendo dalla casella in basso a sinistra
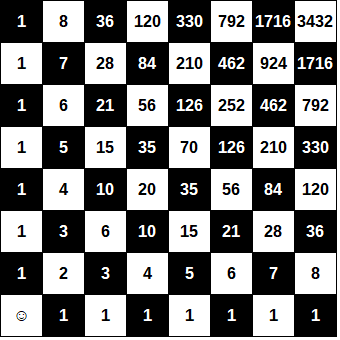

Osserva, il numero di percorsi per raggiungere B e per raggiungere A a partire da B
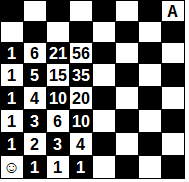

Esercizi
Calcola le probabilità per altre caselle diverse da B
1
Da A1 a H8 passando per B8, (E,N,N,N,N,N,N,N) + (E,E,E,E,E,E)
![]() = 8
= 8
p(—) = ![]() = 0,00233… ~ 0,233 %
= 0,00233… ~ 0,233 %
2
Da A1 a H8 passando per C7, (E,E,N,N,N,N,N,N) + (E,E,E,E,E,N)
![]() = 168
= 168
p(—) = ![]() = 0,04895… ~ 4,895 %
= 0,04895… ~ 4,895 %
3
Da A1 a H8 passando per E5, (E,E,E,E,N,N,N,N) + (E,E,E,N,N,N)
![]() = 1400
= 1400
p(—) = ![]() = 0,4079… ~ 41 %
= 0,4079… ~ 41 %