Esame di Stato 2018 – 8

di

In un gioco a due giocatori, ogni partita vinta frutta 1 punto e vince chi per primo raggiunge 10 punti.
Due giocatori che in ciascuna partita hanno la stessa probabilità di vincere si sfidano.
Qual è la probabilità che uno dei due giocatori vinca in un numero di partite minore o uguale a 12?

Soluzione 1

Considera le probabilità degli eventi che portano alla vittoria di A

  • 10 punti nelle prime 10 partite: \displaystyle {10 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^{0} = \displaystyle \frac{1}{2^{10}}
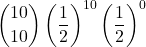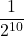
  • 9 punti nelle prime 10 partite e 1 punto nella 11°: \displaystyle {10 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^1 . \displaystyle \frac{1}{2} = … = \displaystyle 10\cdot \frac{1}{2^{11}}
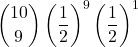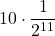
  • 9 punti nelle prime 11 partite e 1 punto nella 12°: \displaystyle {11 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^2 . \displaystyle \frac{1}{2} = … = \displaystyle 55\cdot\frac{1}{2^{12}}
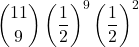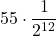
  • (10 punti in 10 partite) oppure
    (9 punti nelle prime 10 partite e 1 punto nella 11°) oppure
    (9 punti nelle prime 11 partite e 1 punto nella 12°)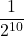
    \displaystyle \frac{1}{2^{10}} + \displaystyle 10\cdot \frac{1}{2^{11}} + \displaystyle 55\cdot\frac{1}{2^{12}} = … = \displaystyle \frac{79}{2^{12}}

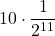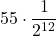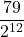
Simmetricamente le sconfitte di A portano a vittorie di B e ripetendo i calcoli si ottiene lo stesso risultato quindi “la probabilità che uno dei due giocatori vinca in un numero di partite minore o uguale a 12” è

\displaystyle 2\cdot\frac{79}{2^{12}} = \displaystyle \frac{79}{2^{11}} ~ 0.0386 = 3.86 %

Soluzione 2

  • 10 punti nelle prime 10 partite: \displaystyle {10 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^{0} = \displaystyle \frac{1}{2^{10}}
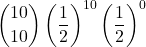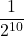
  • 9 punti nelle prime 10 partite e 1 punto nella 11°: \displaystyle {10 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^1 . \displaystyle \frac{1}{2} = … = \displaystyle 10\cdot \frac{1}{2^{11}}
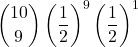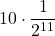
  • 9 punti nelle prime 10 partite, 0 punti nella 11° e 1 punto nella 12°: \displaystyle {11 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^2 . \displaystyle \frac{1}{2} . \displaystyle \frac{1}{2} = … = \displaystyle 10\cdot \frac{1}{2^{12}}
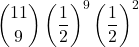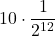
  • 8 punti nelle prime 10 partite, 1 punto nella 11 e 1 punto nella 12°: \displaystyle {10 \choose 8}\left(\frac{1}{2}\right)^{8}\left(\frac{1}{2}\right)^{2} . \displaystyle \frac{1}{2} . \displaystyle \frac{1}{2} = … = \displaystyle 45\cdot\frac{1}{2^{12}}
  • …
    \displaystyle \frac{1}{2^{10}} + \displaystyle 10\cdot \frac{1}{2^{11}} + \displaystyle 10\cdot \frac{1}{2^{12}} + \displaystyle 45\cdot\frac{1}{2^{12}} = … = \displaystyle \frac{79}{2^{12}}
  • …

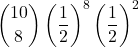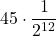
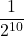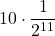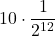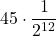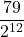
Soluzione 3

Il giocatore A vince in 12 partite se ottiene 10, 11 oppure 12 punti

  • \displaystyle {12 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^2 + \displaystyle {12 \choose 11}\left(\frac{1}{2}\right)^{11}\left(\frac{1}{2}\right)^0 + \displaystyle {12 \choose 12}\left(\frac{1}{2}\right)^{12}\left(\frac{1}{2}\right)^{0}
  • \displaystyle 66\cdot\frac{1}{2^{12}} + \displaystyle 12\cdot\frac{1}{2^{12}} + \displaystyle \frac{1}{2^{12}}
  • \displaystyle \frac{79}{2^{12}}
  • …

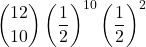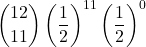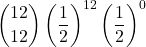
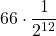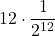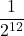
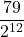
Vedi: Zanichelli.it | Matematica.it

Esercizio

Considera le probabilità del numero di vittorie per ogni numero di partite

 Numero di partite
89101112
Numero
di vittorie
0\displaystyle {8 \choose 0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{8}\displaystyle {9 \choose 0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{9}\displaystyle {10 \choose 0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{10}\displaystyle {11 \choose 0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{11}\displaystyle {12 \choose 0}\left(\frac{1}{2}\right)^{0}\left(\frac{1}{2}\right)^{12}
1\displaystyle {8 \choose 1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{7}\displaystyle {9 \choose 1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{8}\displaystyle {10 \choose 1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{9}\displaystyle {11 \choose 1}\left(\frac{1}{2}\right)^{1}\left(\frac{1}{2}\right)^{10}\displaystyle {12 \choose 1}\left(\frac{1}{2}\right)^1\left(\frac{1}{2}\right)^{11}
2\displaystyle {8 \choose 2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{6}\displaystyle {9 \choose 2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{7}\displaystyle {10 \choose 2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{8}\displaystyle {11 \choose 2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{9}\displaystyle {12 \choose 2}\left(\frac{1}{2}\right)^{2}\left(\frac{1}{2}\right)^{10}
…—————
8\displaystyle {8 \choose 8}\left(\frac{1}{2}\right)^{8}\left(\frac{1}{2}\right)^{0}\displaystyle {9 \choose 8}\left(\frac{1}{2}\right)^{8}\left(\frac{1}{2}\right)^{1}\displaystyle {10 \choose 8}\left(\frac{1}{2}\right)^{8}\left(\frac{1}{2}\right)^{2}——
9—\displaystyle {9 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^{0}\displaystyle {10 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^1\displaystyle {11 \choose 9}\left(\frac{1}{2}\right)^{9}\left(\frac{1}{2}\right)^2—
10——\displaystyle {10 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^{0}\displaystyle {11 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^1\displaystyle {12 \choose 10}\left(\frac{1}{2}\right)^{10}\left(\frac{1}{2}\right)^2
11———\displaystyle {11 \choose 11}\left(\frac{1}{2}\right)^{11}\left(\frac{1}{2}\right)^{0}\displaystyle {12 \choose 11}\left(\frac{1}{2}\right)^{11}\left(\frac{1}{2}\right)^0
12————\displaystyle {12 \choose 12}\left(\frac{1}{2}\right)^{12}\left(\frac{1}{2}\right)^{0}

In sintesi

 Numero di partite
89101112
Numero
di vittorie		0\displaystyle \frac{1}{2^{8}}\displaystyle \frac{1}{2^{9}}\displaystyle \frac{1}{2^{10}}\displaystyle \frac{1}{2^{11}}\displaystyle \frac{1}{2^{12}}
1\displaystyle 8\cdot\frac{1}{2^{8}}\displaystyle 9\cdot\frac{1}{2^{9}}\displaystyle 10\cdot\frac{1}{2^{10}}\displaystyle 11\cdot\frac{1}{2^{11}}\displaystyle 12\cdot\frac{1}{2^{12}}
2\displaystyle 28\cdot\frac{1}{2^{8}}\displaystyle 36\cdot\frac{1}{2^{9}}\displaystyle 45\cdot\frac{1}{2^{10}}\displaystyle 55\cdot\frac{1}{2^{11}}\displaystyle 66\cdot\frac{1}{2^{12}}
…—————
8\displaystyle \frac{1}{2^{8}}\displaystyle 9\cdot\frac{1}{2^{9}}\displaystyle 45\cdot\frac{1}{2^{10}}——
9—\displaystyle \frac{1}{2^{9}}\displaystyle 10\cdot\frac{1}{2^{10}}\displaystyle 55\cdot\frac{1}{2^{11}}—
10——\displaystyle \frac{1}{2^{10}}\displaystyle 11\cdot\frac{1}{2^{11}}\displaystyle 66\cdot\frac{1}{2^{12}}
11———\displaystyle \frac{1}{2^{11}}\displaystyle 12\cdot\frac{1}{2^{12}}
12————\displaystyle \frac{1}{2^{12}}