Esame di Stato 2023 – Quesito 2

di

Un dado truccato, con le facce numerate da 1 a 6, gode della proprietà di avere ciascuna faccia pari che si presenta con probabilità doppia rispetto a ciascuna faccia dispari.

Calcolare le probabilità di ottenere, lanciando una volta il dado, rispettivamente:

  1. un numero primo
  2. un numero almeno pari a 3
  3. un numero al più pari a 3

Osserva

\begin{cases} p_1 = p_3 = p_5 \\ p_2 = p_4 = p_6 \\ p_2 = 2\cdot p_1 \\ p_1+p_2+p_3+p_4+p_5+p_6 = 1 \end{cases}

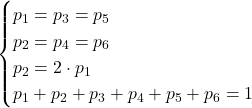
quindi…

\begin{cases} \displaystyle p_1 = p_3 = p_5 = \frac{1}{9} \\ \displaystyle p_2 = p_4 = p_6 = \frac{2}{9} \end{cases}

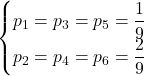
Quesiti

  1. La probabilità che, lanciando una volta un dado, esca un numero primo è
    p_2+p_3+p_5 = \displaystyle \frac{2}{9}+\frac{1}{9}+\frac{1}{9} = \displaystyle \frac{4}{9}
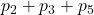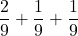  2. La probabilità che, lanciando una volta un dado, esca un numero almeno pari a 3 è
    p_3+p_4+p_5+p_6 = \displaystyle \frac{1}{9}+\frac{2}{9}+\frac{1}{9}+\frac{2}{9} = \displaystyle \frac{6}{9} = \displaystyle \frac{2}{3}
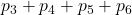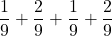  3. La probabilità che, lanciando una volta un dado, esca un numero al più pari a 3 è
    p_1+p_2+p_3 = \displaystyle \frac{1}{9}+\frac{2}{9}+\frac{1}{9} = \displaystyle \frac{4}{9}

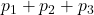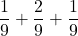Esercizio aggiuntivo 1

Sia X la variabile casuale “punti realizzati lanciando un dado truccato…”, allora

x_ip_ip_i\ x_ix_i^2p_i\ x_i^2(x_i-m)p_i\ (x_i-m)|x_i-m|p_i\ |x_i-m|(x_i-m)^2p_i\ (x_i-m)^2
1\displaystyle \frac{1}{9}\displaystyle \frac{1}{9}1\displaystyle \frac{1}{9}\displaystyle -\frac{8}{3}\displaystyle -\frac{8}{27}\displaystyle \frac{8}{3}\displaystyle \frac{8}{27}\displaystyle \frac{64}{9}\displaystyle \frac{64}{81}
2\displaystyle \frac{2}{9}\displaystyle \frac{4}{9}4\displaystyle \frac{8}{9}\displaystyle -\frac{5}{3}\displaystyle -\frac{10}{27}\displaystyle \frac{5}{3}\displaystyle \frac{10}{27}\displaystyle \frac{25}{9}\displaystyle \frac{50}{81}
3\displaystyle \frac{1}{9}\displaystyle \frac{3}{9}9\displaystyle \frac{9}{9}\displaystyle -\frac{2}{3}\displaystyle -\frac{2}{27}\displaystyle \frac{2}{3}\displaystyle \frac{2}{27}\displaystyle \frac{4}{9}\displaystyle \frac{4}{81}
4\displaystyle \frac{2}{9}\displaystyle \frac{8}{9}16\displaystyle \frac{32}{9}\displaystyle \frac{1}{3}\displaystyle \frac{2}{27}\displaystyle \frac{1}{3}\displaystyle \frac{2}{27}\displaystyle \frac{1}{9}\displaystyle \frac{2}{81}
5\displaystyle \frac{1}{9}\displaystyle \frac{5}{9}25\displaystyle \frac{25}{9}\displaystyle \frac{4}{3}\displaystyle \frac{4}{27}\displaystyle \frac{4}{3}\displaystyle \frac{4}{27}\displaystyle \frac{16}{9}\displaystyle \frac{16}{81}
6\displaystyle \frac{2}{9}\displaystyle \frac{12}{9}36\displaystyle \frac{72}{9}\displaystyle \frac{7}{3}\displaystyle \frac{14}{27}\displaystyle \frac{7}{3}\displaystyle \frac{14}{27}\displaystyle \frac{49}{9}\displaystyle \frac{98}{81}
 1\displaystyle \frac{11}{3}81\displaystyle \frac{49}{3}-109\displaystyle \frac{40}{27}\displaystyle \frac{53}{3}\displaystyle \frac{26}{9}
M(X)M(X^2)\displaystyle \delta(X)\displaystyle dev(x)\displaystyle var(X)

Osserva

Media\displaystyle M(X)= \displaystyle \sum_i p_i\ x_i= \displaystyle \frac{11}{3}= 3,666…
Scarto medio assoluto\displaystyle \delta(X)= \displaystyle \sum _{i}p_i\ |x_{i}-m|}= \displaystyle \frac{40}{27}= 1,48…
Devianza\displaystyle dev(x)= \displaystyle \sum_{i}(x_i-m)^2= \displaystyle \frac{53}{3}= 17,666…
Varianza\displaystyle var(X)= \displaystyle \sum_i p_i\ (x_i-m)^2= \displaystyle \frac{26}{9}= 2,888…
Deviazione standard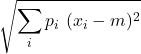\sigma (X)= \displaystyle \sqrt{\sum_i p_i\ (x_i-m)^2}= \displaystyle \frac{\sqrt{26}}{3}= 1,699…
Deviazione standard relativa\displaystyle \sigma^{*}(X)= \displaystyle \frac{\sigma(X)}{|M(X)|}= \displaystyle \frac{\sqrt{26}}{11}= 0,4635…
…\displaystyle M(X^2)= \displaystyle \sum_ip_i\ x_i^2= \displaystyle \frac{49}{3}= 16,333…
Varianzavar(X)= \displaystyle M(X^2)-[M(X)]^2= \displaystyle \frac{49}{3}-\left(\frac{11}{3}\right)^2 = \displaystyle \frac{26}{9}= 2,888…

Esercizio aggiuntivo 2

Sia X la variabile casuale “punti realizzati lanciando due dadi truccati…”, allora

x_ip_i
21+1\displaystyle \frac{1}{9}\cdot \frac{1}{9}= \displaystyle \frac{1}{81}
31+22+1\displaystyle \frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}= \displaystyle \frac{4}{81}
41+32+23+1\displaystyle \frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}= \displaystyle \frac{6}{81}= \displaystyle \frac{2}{27}
51+42+33+24+1\displaystyle \frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}+\frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}= \displaystyle \frac{8}{81}
61+52+43+34+25+1\displaystyle \frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}= \displaystyle \frac{11}{81}
71+62+53+44+35+26+1\displaystyle \frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}+\frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}+\frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}= \displaystyle \frac{12}{81}= \displaystyle \frac{4}{27}
82+63+54+45+36+2\displaystyle \frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}= \displaystyle \frac{14}{81}
93+64+55+46+3\displaystyle \frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}= \displaystyle \frac{8}{81}
104+65+56+4\displaystyle \frac{2}{9}\cdot \frac{2}{9}+\frac{1}{9}\cdot \frac{1}{9}+\frac{2}{9}\cdot \frac{2}{9}= \displaystyle \frac{9}{81}= \displaystyle \frac{1}{9}
115+66+5\displaystyle \frac{1}{9}\cdot \frac{2}{9}+\frac{2}{9}\cdot \frac{1}{9}= \displaystyle \frac{4}{81}
126+6\displaystyle \frac{2}{9}\cdot \frac{2}{9}= \displaystyle \frac{4}{81}
1

Esercizio aggiuntivo 3

Sia X la variabile casuale “punti realizzati lanciando due dadi truccati…”, allora

x_ip_ip_i\ x_ix_i^2p_i\ x_i^2(x_i-m)p_i\ (x_i-m)(x_i-m)^2p_i\ (x_i-m)^2
2\displaystyle \frac{1}{81}\displaystyle \frac{2}{81}4\displaystyle \frac{4}{81}——
3\displaystyle \frac{4}{81}\displaystyle \frac{4}{27}9\displaystyle \frac{4}{9}——
4\displaystyle \frac{2}{27}\displaystyle \frac{8}{27}16\displaystyle \frac{32}{27}——
5\displaystyle \frac{8}{81}\displaystyle \frac{40}{81}25\displaystyle \frac{200}{81}——
6\displaystyle \frac{11}{81}\displaystyle \frac{22}{27}36\displaystyle \frac{44}{9}——
7\displaystyle \frac{4}{27}\displaystyle \frac{28}{27}49\displaystyle \frac{196}{27}——
8\displaystyle \frac{14}{81}\displaystyle \frac{112}{81}64\displaystyle \frac{896}{81}——
9\displaystyle \frac{8}{81}\displaystyle \frac{8}{9}818——
10\displaystyle \frac{1}{9}\displaystyle \frac{10}{9}100\displaystyle \frac{100}{9}——
11\displaystyle \frac{4}{81}\displaystyle \frac{44}{81}121\displaystyle \frac{484}{81}——
12\displaystyle \frac{4}{81}\displaystyle \frac{16}{27}144\displaystyle \frac{64}{9}——
1\displaystyle \frac{22}{3}\displaystyle \frac{536}{9}——
 M(X)M(X^2) var(X)

Osserva

Media\displaystyle M(X)= \displaystyle \sum_i p_i\cdot x_i= \displaystyle \frac{22}{3}= 7,33…
Scarto medio assoluto\displaystyle \delta(X)= \displaystyle \sum _{i}p_i|x_{i}-m|}= …= …
Devianza\displaystyle dev(x)= \displaystyle \sum_{i}(x_i-m)^2= …
Varianza\displaystyle var(X)= \displaystyle \sum_i p_i(x_i-m)^2= …= …
Deviazione standard\sigma (X)= \displaystyle \sqrt{\sum_i p_i(x_i-m)^2}= …= …
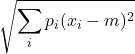Deviazione standard relativa\displaystyle \sigma^{*}(X)= \displaystyle \frac{\sigma(X)}{|M(X)|}= …= …
…\displaystyle M(X^2)= \displaystyle \sum_ip_i\cdot x_i^2= \displaystyle \frac{536}{9}= 59,55…
Varianzavar(X)= \displaystyle M(X^2)-[M(X)]^2= …= …