Flussi in una rete

OPS e Flussi in una rete

Sul fianco di una montagna esistono numerose sorgenti.
L’acqua di una sorgente, che si suppone fluire in modo continuo e costante, può scorrere a valle attraverso uno o più canali.
Può avvenire che uno o più canali convergano in un punto in cui esiste una sorgente; in tal caso, la loro acqua si aggiunge a quella fornita dalla sorgente raggiunta.
Questa situazione è descrivibile con un reticolo di nodi (le sorgenti) collegati da archi (i canali).

La situazione quindi è descritta da due tabelle:

• s(<sorgente>, <litri d’acqua erogata al minuto>), che specifica la quantità d’acqua che sgorga da ogni sorgente (che è un nodo del reticolo),
• r(<sorgente1>, <sorgente2>), che specifica la presenza di un canale che porta acqua dalla sorgente1 alla sorgente2.

Se da una sorgente escono più canali, l’acqua si divide in parti uguali fra ciascuno di essi.

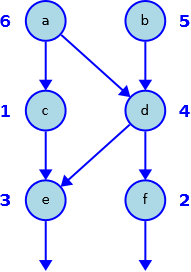
Nella situazione descritta dal seguente esempio (con radici in a e in b, vedi figura)

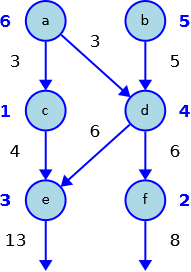
la quantità d’acqua che esce dai nodi e, f è riportata di seguito

• e = 13
• f = 8

ESERCIZIO 1

Un reticolo di canali si può descrivere con due tabelle associate ai seguenti due termini:

• s(<sorgente>, <litri d’acqua erogata al minuto>), che specifica la quantità d’acqua che sgorga da ogni sorgente (che è un nodo del reticolo), e
• r(<sorgente1>, <sorgente2>), che specifica la presenza di un canale che porta acqua dalla sorgente1 alla sorgente2.

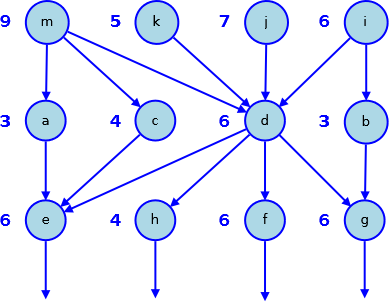
Un reticolo è descritto dalle seguenti due tabelle:

1. s(a, 3)
2. s(b, 3)
3. s(c, 4)
4. s(d, 6)
5. s(e, 6)
6. s(f, 6)
7. s(g, 6)
8. s(h, 4)
9. s(i, 6)
10. s(j, 7)
11. s(k, 5)
12. s(m, 9)

1. r(a, e)
2. r(b, g)
3. r(c, e)
4. r(d, g)
5. r(d, h)
6. r(i, b)
7. r(i, d)
8. r(d, f)
9. r(d, e)
10. r(k, d)
11. r(j, d)
12. r(m, d)
13. r(m, c)
14. r(m, a)

Disegnare il reticolo, evitando incroci tra i rigagnoli, e determinare la quantità di acqua che esce dai nodi e, f, g, h.

SOLUZIONE

Il reticolo di canali, evitando incroci tra i rigagnoli…

e le quantità di acqua (l’acqua che esce da una sorgente si distribuisce equamente nei canali presenti)

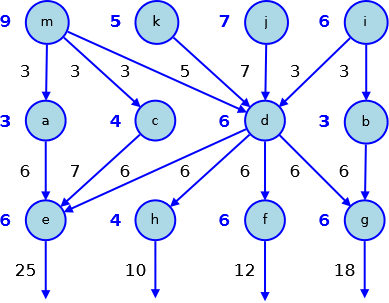
Le risposte

• e = 25
• f = 12
• g = 18
• h = 10

OII 2-12-2010 – Numero 9

Un reticolo è descritto dalle seguenti due sequenze:

1. s(a, 2)
2. s(b, 6)
3. s(c, 4)
4. s(d, 8)
5. s(e, 3)
6. s(f, 2)
7. s(g, 2)
8. s(h, 2)
9. s(i, 12)
10. s(j, 3)
11. s(k, 5)
12. s(m, 1)

1. r(a, e)
2. r(b, e)
3. r(b, f)
4. r(c, f)
5. r(c, g)
6. r(d, g)
7. r(d, h)
8. r(e, i)
9. r(f, j)
10. r(g, j)
11. r(g, m)
12. r(h, m)
13. r(i, k)
14. r(j, k)
15. r(j, m)

Calcolare la quantità di acqua che esce dai nodi k e m.

SOLUZIONE

Il reticolo corrispondente alle due sequenze è

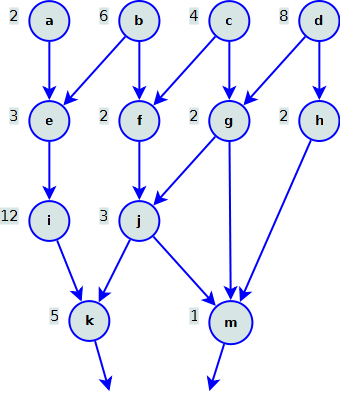
e le quantità di acqua che escono dai nodi

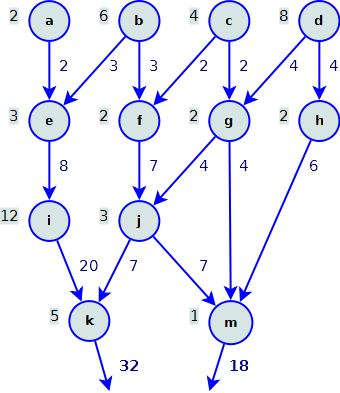
Soluzione: k=32, m=18.

Un reticolo di canali è descritto dalle seguenti due tabelle:

• s(a,3), s(b,6), s(c,6), s(d,2), s(e,1), s(f,10), s(g,3), s(h,4), s(i,1), s(l,3), s(m,1), s(n,10)
• r(a,d), r(b,d), r(b,e), r(c,e), r(d,g), r(e,g), r(f,i), r(g,i), r(g,l), r(g,m), r(h,m), r(i,n), r(l,n), r(m,n)

Disegnare il reticolo, evitando incroci fra i rigagnoli, e determinare la quantità di acqua che esce dai nodi d, g, i, n.

Un reticolo di canali è descritto dalle seguenti due tabelle:

• s(a,8), s(b,4), s(c,2), s(d,6), s(e,4), s(f,10), s(g,1), s(h,1), s(i,10), s(l,2), s(m,2)
• r(a,b), r(b,c), r(b,d), r(c,e), r(d,e), r(d,f), r(e,g), r(f,g), r(f,h), r(g,h), r(d,i), r(i,f), r(i,l), r(f,l), r(l,h), r(l,m), r(h,m)

Disegnare il reticolo, evitando incroci fra i rigagnoli, e determinare la quantità di acqua che esce dai nodi d, h, i, m.

• s(a,4), s(b,2), s(c,8), s(d,4), s(e,1), s(f,2), s(g,2), s(h,2), s(i,10), s(j,5)
• r(a,c), r(a,d), r(b,d), r(b,e), r(c,d), r(d,e), r(c,f), r(d,f), r(d,g), r(d,h), r(e,h), r(f,i), r(g,f), r(g,i), r(h,g), r(i,j), r(h,j)