Matrice inversa

di
Algebra lineare

La matrice inversa A^{-1} di una matrice quadrata A gode delle proprietà

  1. A^{-1}\cdot A = I = A\cdot A^{-1}
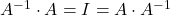
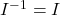  2. I^{-1} = I, l’inversa della matrice identità e la matrice identità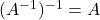
  3. (A^{-1})^{-1} = A
  4. (A\cdot B)^{-1} = B^{-1}\cdot A^{-1}
  5. \displaystyle \det(A^{-1}) = \frac{1}{\det(A)}
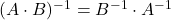
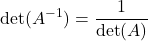
  6. Una matrice quadrata A è invertibile se e solo se il determinante non è nullo.
  7. Se A è triangolare lo è anche A^{-1}
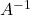
  8. Se A è diagonale lo è anche A^{-1}
  9. …

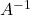
Con la matrice inversa di A si calcola la soluzione del sistema lineare Ax = b.

Calcolo della matrice inversa