Polinomio di Lagrange – 100

di
Radici e zeri

Esercizio del libro di testo a pagina 100.
Calcola il valore approssimato per x=3 utilizzando il polinomio interpolatore di Lagrange passante per i punti dati.
Svolgi l’esercizio per 2 / 3 / 4 / 5 / 6 punti.

Punti = 2, Grado = 1

xy
02-3
1115
p_1(x)= y_0 \cdot L_0(x) +y_1\cdot L_1(x)
= y_0 \cdot \displaystyle \frac{x-x_1}{x_0-x_1} +y_1\cdot \displaystyle \frac{x-x_0}{x_1-x_0}
= -3 \cdot \displaystyle \frac{x-1}{2-1} +15\cdot \displaystyle \frac{x-2}{1-2}
p_1(3)= -3 \cdot \displaystyle \frac{3-1}{2-1} +15\cdot \displaystyle \frac{3-2}{1-2}
= -3 \cdot \displaystyle \frac{2}{1} +15\cdot \displaystyle \frac{1}{-1} = -6-15 = -21

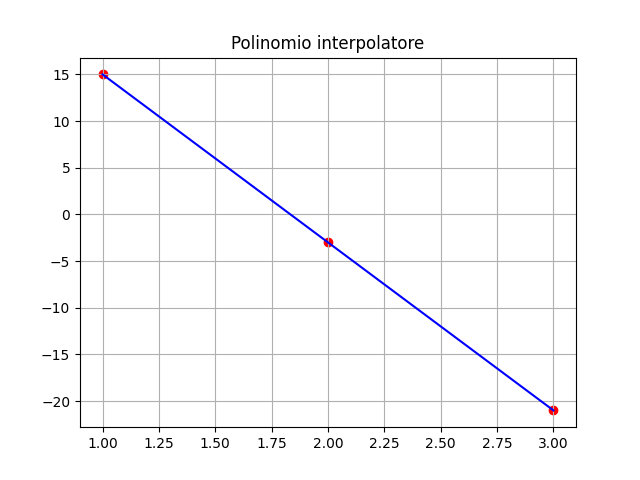
Punti = 3, Grado = 2

xy
02-3
1115
252
p_2(x)= y_0 \cdot L_0(x) + y_1\cdot L_1(x) + y_2\cdot L_2(x)
= y_0 \cdot \displaystyle \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} + y_1\cdot \displaystyle \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} + y_2\cdot \displaystyle \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}
= -3 \cdot \displaystyle \frac{(x-1)(x-5)}{(2-1)(2-5)} +15\cdot \displaystyle \frac{(x-2)(x-5)}{(1-2)(1-5)} +2 \cdot \displaystyle \frac{(x-2)(x-1)}{(5-2)(5-1)}
p_2(3)= -3 \cdot \displaystyle \frac{(3-1)(3-5)}{(2-1)(2-5)} +15\cdot \displaystyle \frac{(3-2)(3-5)}{(1-2)(1-5)} +2 \cdot \displaystyle \frac{(3-2)(3-1)}{(5-2)(5-1)}
= -3 \cdot \displaystyle \frac{(2)(-2)}{(1)(-3)} +15\cdot \displaystyle \frac{(1)(-2)}{(-1)(-4)} +2 \cdot \displaystyle \frac{(1)(2)}{(3)(4)}
= -3 \cdot \displaystyle \frac{-4}{-3} +15\cdot \displaystyle \frac{-2}{4} +2 \cdot \displaystyle \frac{2}{12} = \displaystyle -4-\frac{15}{2}+\frac{1}{3} = \displaystyle -\frac{67}{6} = -11,166…

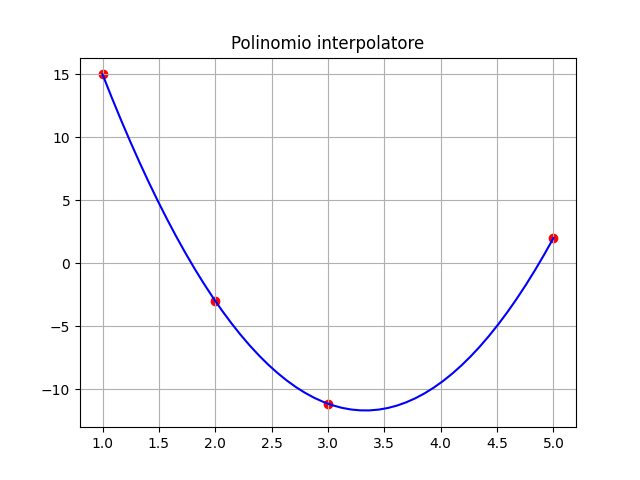
Punti = 4, Grado = 3

xy
02-3
1115
252
361
p_3(x)= y_0 \cdot L_0(x) + y_1\cdot L_1(x) + y_2\cdot L_2(x) + y_3\cdot L_3(x)
= y_0 \cdot \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} + y_1\cdot \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} + y_2\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}
+ y_3\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_2-x_0)(x_2-x_1)(x_2-x_2)}
= -3 \cdot \displaystyle \frac{(x-1)(x-5)(x-6)}{(2-1)(2-5)(2-6)} +15\cdot \displaystyle \frac{(x-2)(x-5)(x-6)}{(1-2)(1-5)(1-6)} +2 \cdot \displaystyle \frac{(x-2)(x-1)(x-6)}{(5-2)(5-1)(5-6)}
+1 \cdot \displaystyle \frac{(x-2)(x-1)(x-5)}{(6-2)(6-1)(6-5)}
p_3(3)= -3 \cdot \displaystyle \frac{(3-1)(3-5)(3-6)}{(2-1)(2-5)(2-6)} +15\cdot \displaystyle \frac{(3-2)(3-5)(3-6)}{(1-2)(1-5)(1-6)} +2 \cdot \displaystyle \frac{(3-2)(3-1)(3-6)}{(5-2)(5-1)(5-6)}
+1 \cdot \displaystyle \frac{(3-2)(3-1)(3-5)}{(6-2)(6-1)(6-5)}
= -3 \cdot \displaystyle \frac{(2)(-2)(-3)}{(1)(-3)(-4)} +15\cdot \displaystyle \frac{(1)(-2)(-3)}{(-1)(-4)(-5)} +2 \cdot \displaystyle \frac{(1)(2)(-3)}{(3)(4)(-1)} +1 \cdot \displaystyle \frac{(1)(2)(-2)}{(4)(5)(1)}
= -3 \cdot \displaystyle \frac{12}{12} +15\cdot \displaystyle \frac{6}{-20} +2 \cdot \displaystyle \frac{-6}{-12} +1 \cdot \displaystyle \frac{-4}{20} = \displaystyle -3-\frac{9}{2}+1-\frac{1}{5} = \displaystyle -\frac{67}{10} = -6,7

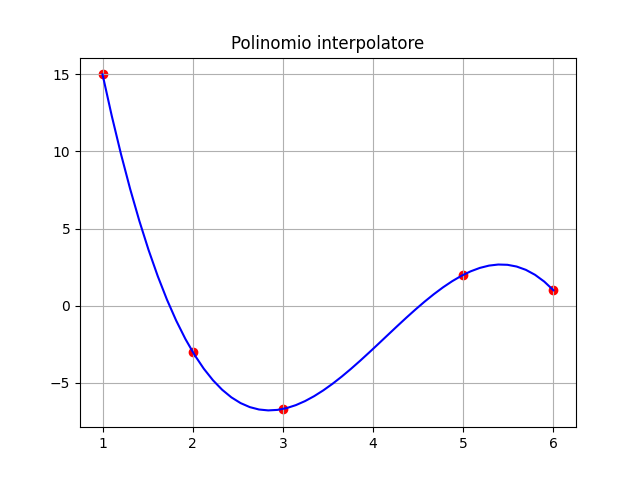
Punti = 5, Grado = 4

xy
02-3
1115
252
361
440
p_4(x)= y_0 \cdot L_0(x) + y_1\cdot L_1(x) + y_2\cdot L_2(x) + y_3\cdot L_3(x) + y_4\cdot L_4(x)
= y_0 \cdot \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)} +y_1\cdot \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)}
+ y_2\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)} +y_3\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)}
+y_4\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)}{(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)}
= -3 \cdot \displaystyle \frac{(x-1)(x-5)(x-6)(x-4)}{(2-1)(2-5)(2-6)(2-4)} +15 \cdot \displaystyle \frac{(x-2)(x-5)(x-6)(x-4)}{(1-2)(1-5)(1-6)(1-4)}
+2 \cdot \displaystyle \frac{(x-2)(x-1)(x-6)(x-4)}{(5-2)(5-1)(5-6)(5-4)} + 1 \cdot \displaystyle \frac{(x-2)(x-1)(x-5)(x-4)}{(6-2)(6-1)(6-5)(6-4)}
+ 0 \cdot \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)}{(4-2)(4-1)(4-5)(4-6)}
p_4(3)= -3 \cdot \displaystyle \frac{(3-1)(3-5)(3-6)(3-4)}{(2-1)(2-5)(2-6)(2-4)} +15 \cdot \displaystyle \frac{(3-2)(3-5)(3-6)(3-4)}{(1-2)(1-5)(1-6)(1-4)}
+2 \cdot \displaystyle \frac{(3-2)(3-1)(3-6)(3-4)}{(5-2)(5-1)(5-6)(5-4)} + 1 \cdot \displaystyle \frac{(3-2)(3-1)(3-5)(3-4)}{(6-2)(6-1)(6-5)(6-4)}
+ 0 \cdot \displaystyle \frac{(3-2)(3-1)(3-5)(3-6)}{(4-2)(4-1)(4-5)(4-6)}
= -3 \cdot \displaystyle \frac{(2)(-2)(-3)(-1)}{(1)(-3)(-4)(-2)} +15 \cdot \displaystyle \frac{(1)(-2)(-3)(-1)}{(-1)(-4)(-5)(-3)} +2 \cdot \displaystyle \frac{(1)(2)(-3)(-1)}{(3)(4)(-1)(1)} + 1 \cdot \displaystyle \frac{(1)(2)(-2)(-1)}{(4)(5)(1)(2)} + 0 \cdot \displaystyle \frac{(1)(2)(-2)(-3)}{(2)(3)(-1)(-2)}
= -3 \cdot \displaystyle \frac{-12}{-24} +15 \cdot \displaystyle \frac{-6}{60} +2 \cdot \displaystyle \frac{6}{-12} + 1 \cdot \displaystyle \frac{4}{40} + 0 \cdot \displaystyle \frac{12}{12} = -\displaystyle \frac{3}{2} - \displaystyle \frac{3}{2}-1 + \displaystyle \frac{1}{10}+ 0 = \displaystyle -\frac{39}{10} = -3,9

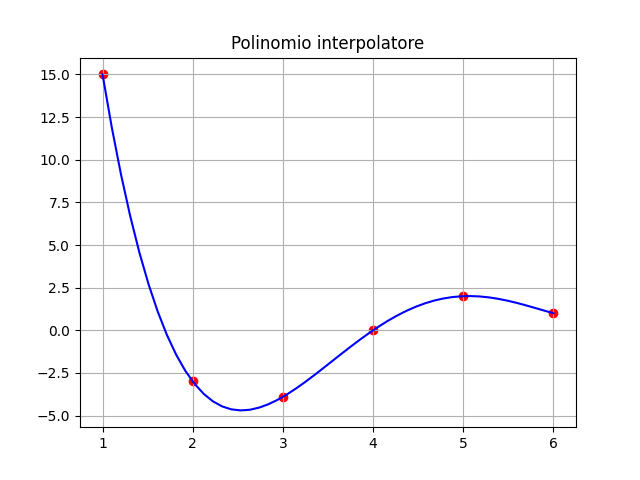
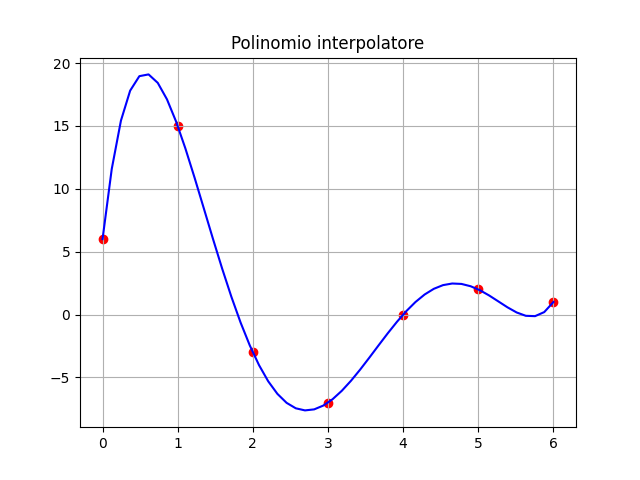
Punti = 6, Grado = 5

xy
02-3
1115
252
361
440
506
p_5(x)= y_0 \cdot L_0(x) + y_1\cdot L_1(x) + y_2\cdot L_2(x) + y_3\cdot L_3(x) + y_4\cdot L_4(x) + y_5\cdot L_5(x)
= y_0 \cdot \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)(x_0-x_5)} +y_1\cdot \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)}
+ y_2\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)(x-x_5)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)(x_2-x_5)} +y_3\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)(x-x_5)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)(x_3-x_5)}
+y_4\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_5)}{(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)(x_4-x_5)} +y_5\cdot \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_4)}{(x_5-x_0)(x_5-x_1)(x_5-x_2)(x_5-x_3)(x_5-x_4)}
= -3 \cdot \displaystyle \frac{(x-1)(x-5)(x-6)(x-4)(x-0)}{(2-1)(2-5)(2-6)(2-4)(2-0)} +15\cdot \displaystyle \frac{(3-2)(3-5)(3-6)(3-4)(3-0)}{(1-2)(1-5)(1-6)(1-4)(1-0)}
+2\cdot \displaystyle \frac{(x-2)(x-1)(x-6)(x-4)(x-0)}{(5-2)(5-1)(5-6)(5-4)(5-0)} +1\cdot \displaystyle \frac{(x-2)(x-1)(x-5)(x-4)(x-0)}{(6-2)(6-1)(6-5)(6-4)(6-0)}
+0\cdot \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)(x-0)}{(4-2)(4-1)(4-5)(4-6)(4-0)} +6\cdot \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)(x-4)}{(0-2)(0-1)(0-5)(0-6)(0-4)}
p_5(3)= -3 \cdot \displaystyle \frac{(3-1)(3-5)(3-6)(3-4)(3-0)}{(2-1)(2-5)(2-6)(2-4)(2-0)} +15\cdot \displaystyle \frac{(3-2)(3-5)(3-6)(3-4)(3-0)}{(1-2)(1-5)(1-6)(1-4)(1-0)}
+2\cdot \displaystyle \frac{(3-2)(3-1)(3-6)(3-4)(3-0)}{(5-2)(5-1)(5-6)(5-4)(5-0)} +1\cdot \displaystyle \frac{(3-2)(3-1)(3-5)(3-4)(3-0)}{(6-2)(6-1)(6-5)(6-4)(6-0)}
+0\cdot \displaystyle \frac{(3-2)(3-1)(3-5)(3-6)(3-0)}{(4-2)(4-1)(4-5)(4-6)(4-0)} +6\cdot \displaystyle \frac{(3-2)(3-1)(3-5)(3-6)(3-4)}{(0-2)(0-1)(0-5)(0-6)(0-4)}
= -3 \cdot \displaystyle \frac{(2)(-2)(-3)(-1)(3)}{(2)(-3)(-4)(-2)(2)} +15\cdot \displaystyle \frac{(1)(-2)(-3)(-1)(3)}{(-1)(-4)(-5)(-3)(1)} +2\cdot \displaystyle \frac{(1)(2)(-3)(-1)(3)}{(3)(4)(-1)(1)(5)}
+1\cdot \displaystyle \frac{(1)(2)(-2)(-1)(3)}{(4)(5)(1)(2)(6)} +0\cdot \displaystyle \frac{(1)(2)(-2)(-3)(3)}{(2)(3)(-1)(-2)(4)} +6\cdot \displaystyle \frac{(1)(2)(-2)(-3)(-1)}{(-2)(-1)(-5)(-6)(-4)}
= -3 \cdot \displaystyle \frac{-36}{-48} +15\cdot \displaystyle \frac{-18}{60} +2\cdot \displaystyle \frac{18}{-60}+1\cdot \displaystyle \frac{12}{240} +0\cdot \displaystyle \frac{36}{48}+6\cdot \displaystyle \frac{-12}{-240} = \displaystyle -\frac{9}{4}-\frac{9}{2}-\frac{3}{5}+\frac{1}{20}+0+\frac{3}{10} = -7,0

Ripeti gli esercizi calcolando il polinomio interpolatore per 2 / 3 / 4 / 5 / 6 punti

Punti = 2, Grado = 1

xy
02-3
1115
L_0(x)= \displaystyle \frac{x-x_1}{x_0-x_1} = \displaystyle \frac{x-1}{2-1} = \displaystyle x-1
L_1(x)= \displaystyle \frac{x-x_0}{x_1-x_0} = \displaystyle \frac{x-2}{1-2} = \displaystyle -(x-2)
p_1(x)= y_0 \cdot L_0(x) +y_1\cdot L_1(x)
= -3 (x-1) +15\left(-(x-2)\right)
= -18x+33

Punti = 3, Grado = 2

xy
02-3
1115
252
L_0(x)= \displaystyle \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} = \displaystyle \frac{(x-1)(x-5)}{(2-1)(2-5)} = \displaystyle \frac{x^2-6x+5}{-3} = \displaystyle -\frac{1}{3}x^2+2x-\frac{5}{3}
L_1(x)= \displaystyle \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} = \displaystyle \frac{(x-2)(x-5)}{(1-2)(1-5)} = \displaystyle \frac{x^2-7x+10}{4} = \displaystyle \frac{1}{4}x^2-\frac{7}{4}x+\frac{5}{2}
L_2(x)= \displaystyle \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} = \displaystyle \frac{(x-2)(x-1)}{(5-2)(5-1)} = \displaystyle \frac{x^2-3x+2}{12} = \displaystyle \frac{1}{12}x^2-\frac{1}{4}x+\frac{1}{6}
p_2(x)= y_0 \cdot L_0(x) +y_1\cdot L_1(x) +y_2\cdot L_2(x)
= -3\left(\displaystyle -\frac{1}{3}x^2+2x-\frac{5}{3}\right) +15\left(\displaystyle \frac{1}{4}x^2-\frac{7}{4}x+\frac{5}{2} \right) +2 \left(\displaystyle \frac{1}{12}x^2-\frac{1}{4}x+\frac{1}{6} \right)
= \displaystyle \frac{59}{12} x^2 - \frac{131}{4}x + \frac{257}{6}

Punti = 4, Grado = 3

xy
02-3
1115
252
361
L_0(x)= \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}= \displaystyle \frac{(x-1)(x-5)(x-6)}{(2-1)(2-5)(2-6)}
…= \displaystyle \frac{1}{12}\ x^3 -x^2 + \frac{41}{12}x-\frac{5}{2}
L_1(x)= \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)}= \displaystyle \frac{(x-2)(x-5)(x-6)}{(1-2)(1-5)(1-6)}
…= \displaystyle -\frac{1}{20} x^3 + \frac{13}{20}x^2 - \frac{13}{5}x+3
L_2(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)}= \displaystyle \frac{(x-2)(x-1)(x-6)}{(5-2)(5-1)(5-6)}
…= \displaystyle -\frac{1}{12} x^3+ \frac{3}{4}x^2 - \frac{5}{3}x+1
L_3(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)}= \displaystyle \frac{(x-2)(x-1)(x-5)}{(6-2)(6-1)(6-5)}
…= \displaystyle \frac{1}{20} x^3 - \frac{2}{5}x^2 + \frac{17}{20}x- \frac{1}{2}
p_3(x)= y_0 \cdot L_0(x) + y_1 \cdot L_1(x) + y_2 \cdot L_2(x) + y_3 \cdot L_3(x)
= -3 \left(\displaystyle \frac{1}{12} x^3 -x^2 + \frac{41}{12}x-\frac{5}{2} \right) +15 \left(\displaystyle -\frac{1}{20} x^3 + \frac{13}{20}x^2 - \frac{13}{5}x+3 \right) +2 \left(\displaystyle -\frac{1}{12}\ x^3+ \frac{3}{4}x^2 - \frac{5}{3}x+1 \right)
+ \left(\displaystyle \frac{1}{20} x^3 - \frac{2}{5}x^2 + \frac{17}{20}x- \frac{1}{2} \right)
= \displaystyle -\frac{67}{60} x^3 + \frac{277}{20}x^2 - \frac{776}{15}x+54

Punti = 5, Grado = 4

xy
02-3
1115
252
361
440
L_0(x)= \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)}= \displaystyle \frac{(x-1)(x-5)(x-6)(x-4)}{(2-1)(2-5)(2-6)(2-4)}
= …= \displaystyle -\frac{1}{24} x^4 +\frac{2}{3} x^3 -\frac{89}{24} x^2 +\frac{97}{12} x - 5
L_1(x)= \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)}= \displaystyle \frac{(x-2)(x-5)(x-6)(x-4)}{(1-2)(1-5)(1-6)(1-4)}
= …= \displaystyle \frac{1}{60} x^4 -\frac{17}{60} x^3 +\frac{26}{15} x^2 -\frac{67}{15} x + 4
L_2(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)}= \displaystyle \frac{(x-2)(x-1)(x-6)(x-4)}{(5-2)(5-1)(5-6)(5-4)}
= …= \displaystyle -\frac{1}{12} x^4 +\frac{13}{12} x^3 -\frac{14}{3} x^2 +\frac{23}{3} x - 4
L_3(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)}= \displaystyle \frac{(x-2)(x-1)(x-5)(x-4)}{(6-2)(6-1)(6-5)(6-4)}
= …= \displaystyle \frac{1}{40} x^4 -\frac{3}{10} x^3 +\frac{49}{40} x^2 -\frac{39}{20} x + 1
L_4(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)}{(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)}= \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)}{(4-2)(4-1)(4-5)(4-6)}
= …= \displaystyle \frac{1}{12} x^4 -\frac{7}{6} x^3 +\frac{65}{12} x^2 -\frac{28}{3} x + 5
p_4(x)= y_0 \cdot L_0(x) + y_1 \cdot L_1(x) + y_2 \cdot L_2(x) + y_3 \cdot L_3(x) + y_4 \cdot L_4(x)
= -3 \left(\displaystyle -\frac{1}{24} x^4 +\frac{2}{3} x^3 -\frac{89}{24} x^2 +\frac{97}{12} x - 5 \right) +15 \left(\displaystyle \frac{1}{60} x^4 -\frac{17}{60} x^3 +\frac{26}{15} x^2 -\frac{67}{15} x + 4 \right)
+2 \left(\displaystyle -\frac{1}{12} x^4 +\frac{13}{12} x^3 -\frac{14}{3} x^2 +\frac{23}{3} x - 4 \right) + \left( \displaystyle \frac{1}{40} x^4 -\frac{3}{10} x^3 +\frac{49}{40} x^2 -\frac{39}{20} x + 1 \right)
+0 \left(\displaystyle \frac{1}{12} x^4 -\frac{7}{6} x^3 +\frac{65}{12} x^2 -\frac{28}{3} x + 5 \right)
= \displaystyle \frac{7}{30} x^4 -\frac{263}{60} x^3 +\frac{1741}{60} x^2 -\frac{1168}{15} x + 68

Punti = 6, Grado = 5

xy
02-3
1115
252
361
440
506
L_0(x)= \displaystyle \frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)(x_0-x_5)}= \displaystyle \frac{(x-1)(x-5)(x-6)(x-4)(x-0)}{(2-1)(2-5)(2-6)(2-4)(2-0)}
= \displaystyle \frac{x^5-16x^4 +89x^3 +120x}{-48}= \displaystyle -\frac{1}{48}x^5 +\frac{1}{3}x^4 -\frac{89}{48}x^3 +\frac{97}{24}x^2 -\frac{5}{2}x
L_1(x)= \displaystyle \frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)}= \displaystyle \frac{(x-2)(x-5)(x-6)(x-4)(x-0)}{(1-2)(1-5)(1-6)(1-4)(1-0)}
= \displaystyle \frac{x^5-17x^4 +104x^3 -268x^2+240x}{60}= \displaystyle \frac{1}{60}x^5 -\frac{17}{60}x^4 +\frac{26}{15}x^3 -\frac{67}{15}x^2 +4 x
L_2(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)(x-x_5)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)(x_2-x_5)}= \displaystyle \frac{(x-2)(x-1)(x-6)(x-4)(x-0)}{(5-2)(5-1)(5-6)(5-4)(5-0)}
= \displaystyle \frac{x^5-13x^4 +56x^3 -92x^2+48x}{-60}= \displaystyle -\frac{1}{60}x^5 +\frac{13}{60}x^4 -\frac{14}{15}x^3 +\frac{23}{15}x^2 -\frac{4}{5}x
L_3(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)(x-x_5)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)(x_3-x_5)}= \displaystyle \frac{(x-2)(x-1)(x-5)(x-4)(x-0)}{(6-2)(6-1)(6-5)(6-4)(6-0)}
= \displaystyle \frac{x^5-12x^4 +49x^3 -78x^2+40x}{240}= \displaystyle \frac{1}{240}x^5 -\frac{1}{20}x^4 +\frac{49}{240}x^3 -\frac{13}{40}x^2 +\frac{1}{6}x
L_4(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_5)}{(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)(x_4-x_5)}= \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)(x-0)}{(4-2)(4-1)(4-5)(4-6)(4-0)}
= \displaystyle \frac{x^5-14x^4 +65x^3 +122x^2+60x}{48}= \displaystyle \frac{1}{48}x^5 -\frac{7}{24}x^4 +\frac{65}{48}x^3 -\frac{7}{3}x^2 +\frac{5}{4}x
L_5(x)= \displaystyle \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_4)}{(x_5-x_0)(x_5-x_1)(x_5-x_2)(x_5-x_3)(x_5-x_4)}= \displaystyle \frac{(x-2)(x-1)(x-5)(x-6)(x-4)}{(0-2)(0-1)(0-5)(0-6)(0-4)}
= \displaystyle \frac{x^5-18x^4 +121x^3 -372x^2+508x-240}{-240}= \displaystyle -\frac{1}{240}x^5 +\frac{3}{40}x^4 -\frac{121}{240}x^3 +\frac{31}{20}x^2 -\frac{127}{60}x+1
p_5(x)= y_0 \cdot L_0(x) + y_1 \cdot L_1(x) + y_2 \cdot L_2(x) + y_3 \cdot L_3(x) + y_4 \cdot L_4(x) + y_5 \cdot L_5(x)
= -3 \left( \displaystyle -\frac{1}{48}x^5 +\frac{1}{3}x^4 -\frac{89}{48}x^3 +\frac{97}{24}x^2 -\frac{5}{2}x \right) +15 \left(\displaystyle \frac{1}{60}x^5 -\frac{17}{60}x^4 +\frac{26}{15}x^3 -\frac{67}{15}x^2 +4 x\right)
+2 \left(\displaystyle -\frac{1}{60}x^5 +\frac{13}{60}x^4 -\frac{14}{15}x^3 +\frac{23}{15}x^2 -\frac{4}{5}x\right) + \left(\displaystyle \frac{1}{240}x^5 -\frac{1}{20}x^4 +\frac{49}{240}x^3 -\frac{13}{40}x^2 +\frac{1}{6}x\right)
+0 \left(\displaystyle \frac{1}{48}x^5 -\frac{7}{24}x^4 +\frac{65}{48}x^3 -\frac{7}{3}x^2 +\frac{5}{4}x\right) +6 \left(\displaystyle -\frac{1}{240}x^5 +\frac{3}{40}x^4 -\frac{121}{240}x^3 +\frac{31}{20}x^2 -\frac{127}{60}x+1\right)
= \displaystyle \frac{31}{120}\ x^5 - \frac{53}{12}\ x^4 + \frac{215}{8}\ x^3 -\frac{805}{12}\ x^2 + \frac{1601}{30}\ x + 6

Osserva i risultati successivi

PuntiPolinomiox=3
2p_1(x) = -18x+33-21
3p_2(x) = \displaystyle \frac{59}{12} x^2 - \frac{131}{4}x + \frac{257}{6}-11,166…
4p_3(x) = \displaystyle -\frac{67}{60} x^3 + \frac{277}{20}x^2 - \frac{776}{15}x+54-6,7
5p_4(x) = \displaystyle \frac{7}{30} x^4 -\frac{263}{60} x^3 +\frac{1741}{60} x^2 -\frac{1168}{15} x + 68-3,9
6p_5(x) = \displaystyle \frac{31}{120}\ x^5 - \frac{53}{12}\ x^4 + \frac{215}{8}\ x^3 -\frac{805}{12}\ x^2 + \frac{1601}{30}\ x + 6-7