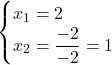Considera il sistema lineare
![]()

Applica l’eliminazione di Gauss alla matrice A affiancata da b

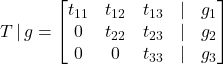
Si ottiene un sistema, con le stesse soluzioni, che può essere risolto calcolando i valori delle variabili partendo dal basso e sostituendo, verso l’alto, i valori ottenuti

Applicando la stessa manipolazione (moltiplicazione per una matrice G) a entrambi i membri si ottiene un sistema equivalente.
Eliminazione di Gauss-Jordan
Se si applicano le manipolazioni che trasformano A in una matrice diagonale la fase finale risulta ancora più semplice

Esempio 2×2
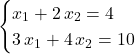
![]()
![]()
![]()
![]()
Dopo l’eliminazione di Gauss
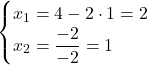
![]()
Altrimenti, continua con l’eliminazione di Jordan
![]()
![]()
![]()