Per calcolare la soluzione di un sistema lineare è sufficiente calcolare la matrice inversa ![]() e dopo il prodotto
e dopo il prodotto ![]()
Esempio 2×2
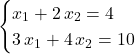
![]()
![]()
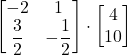 =
= 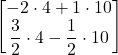
= ![]() =
= ![]()
Se l’inversa è nota: 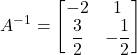
![]()
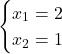
Esempio 3×3
…
Materiali didattici che utilizzo per integrare i libri di testo, motivare e/o distrarre i miei studenti.
Per calcolare la soluzione di un sistema lineare è sufficiente calcolare la matrice inversa ![]() e dopo il prodotto
e dopo il prodotto ![]()
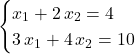
![]()
![]()
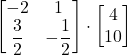 =
= 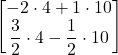
= ![]() =
= ![]()
Se l’inversa è nota: 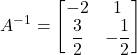
![]()
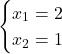
…