1
Bart e Aldo lavorano come camerieri per la Presidenza del Consiglio, ma sono agenti segreti al servizio di governi stranieri, e cercano di rubare documenti riservati.
Bart è al soldo del governo della Sarassonia, Aldo al soldo del governo della Cobadia.
Un documento rubato impiega 4 giorni per raggiungere il governo della Sarassonia e 5 giorni per raggiungere il governo della Cobadia.
Sappiamo le seguenti informazioni:
- Bart riceve un documento riservato il 19 e uno il 22 Ottobre
- Aldo riceve un documento riservato il 21 Ottobre.
- Aldo e Bart pranzano insieme il 20 Ottobre
Sappiamo inoltre che gli agenti segreti non trasmettono documenti direttamente ad altri governi, però possono vendere o rubare documenti da altri agenti segreti e poi trasmetterli al proprio governo.
Se un agente trasmette un documento, lo trasmette il giorno stesso in cui lo ha ricevuto.
Un documento top-secret viene ricevuto dalla Cobadia il 25 di Ottobre.
Il documento è stato:
- rubato e spedito da Bart
- rubato e spedito da Aldo
- rubato da Aldo e venduto a Bart che lo ha spedito
- rubato da Bart e venduto a Aldo che lo ha spedito.
SOLUZIONE
Il problema è lungo e vale solo un punto…
Metti tutto in ordine
| … | Bart è al soldo del governo della Sarassonia. Aldo al soldo del governo della Cobadia. |
| 19/10 | Bart riceve un documento riservato. |
| 20/10 | Aldo e Bart pranzano insieme. Il documento viene spedito. |
| 21/10 | … |
| 22/10 | Bart riceve un documento riservato. |
| 23/10 | … |
| 24/10 | … |
| 25/10 | Il documento viene ricevuto dalla Cobadia |
Il 19/10 Bart riceve un documento riservato, il 20/10 lo vende ad Aldo che lo spedisce il giorno stesso alla Cobadia
 2
2
Quest’anno, la quota di iscrizione alla palestra ICS è aumentata del 10% rispetto allo scorso anno, ma le iscrizioni sono diminuite del 10%.
A proposito dei ricavi che la palestra ICS ha ottenuto quest’anno dalle quote di iscrizione, è vero che:
- sono diminuiti dell’1%
- sono aumentati dell’1%
- sono rimasti uguali
- non si può affermare nulla con certezza senza conoscere la quota di iscrizione e il numero di iscritti dello scorso anno.
3 <–
In un’urna sono contenute 100 palline numerate dall’1 al 100.
Si estrae una pallina dall’urna.
Supposto che le palline abbiano tutte uguale probabilità di essere estratte, qual è la probabilità che la pallina estratta sia un quadrato perfetto minore stretto di 49 (si ricordi che anche 1 è un quadrato perfetto).
- 3/50
- 1/2
- 1/48
- 1/24.
4
Considera il numero a=125032–124972.
Quale delle seguenti affermazioni è vera?
- 10 < a < 102
- 108 < a < 109
- 105 < a < 106
- a è esattamente una potenza di 10.
SOLUZIONE
Ricorda: x2 – y2 = (x – y) · (x + y)
125032 – 124972 = (12503 – 12497) · (12503 + 12497) = 6 · 25.000 = 150.000 = 1,5 · 105
Soluzione: (105 < a < 106)
 5
5
I finanzieri dell’aeroporto di Ario al Faceto (Drago, Franchi, Jerace, Mosca e Patané) sono molto abili nel loro mestiere, tanto che nell’ultima settimana ciascuno di loro ha arrestato uno dei seguenti contrabbandieri: i signori Buboli, Casacci e Cocchi, la signora Leone e la signorina Riccoboni;
e sequestrato una delle seguenti merci:
- cocaina, diamanti, hashish, oppio e oro,
- ciascuna delle quali trovata in uno dei seguenti nascondigli:
- un beauty case, un cappellino, una giacca, un ombrello, una valigia.
In base alle informazioni seguenti, indicare quale contrabbandiere è stato arrestato dal finanziere Drago, cosa cercava di contrabbandare e quale nascondiglio aveva scelto a tale scopo.
- Il finanziere Jerace ha fermato l’uomo che tentava di contrabbandare dei diamanti (che però non erano nascosti nel manico di una valigia);
- il finanziere Mosca ha arrestato la donna che aveva occultato qualcosa nel manico di un ombrello;
- la signora Leone aveva sistemato qualcosa dietro la fodera del proprio cappellino: non si trattava di oro, e ad occuparsi di lei non è stato il finanziere Drago;
- l’arrestato che aveva nascosto l’oppio in un beauty case non era la signorina Riccoboni;
- il signor Casacci è stato fermato dal finanziere Patanè;
- il signor Cocchi nascondeva dell’hashish, ma non nel manico di un ombrello.
 13
13
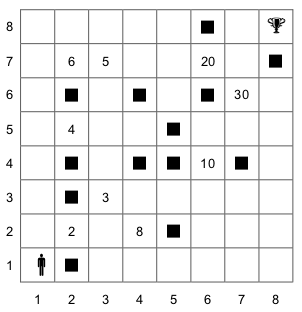
Il pirata Barbagialla trova un’antica mappa che spiega come raggiungere un favoloso tesoro.
La mappa ha la forma di una matrice di celle; le celle possono essere vuote, contenere ostacoli che impediscono a Barbagialla di attraversarle, oppure premi (costituiti da un certo numero di ghinee d’oro); una cella contiene il tesoro.
Con riferimento alla figura, il pirata Barbagialla (la sagoma umana) si trova nella cella individuata dalle coordinate (1,1).
Il tesoro, rappresentato da una coppa, è nella cella (8,8); il campo contiene ostacoli, individuati da quadrati neri posti in 13 celle.
Nove celle contengono dei premi: ad esempio 8 ghinee d’oro nella cella di coordinate (4,2) e 10 nella cella (6,4).
Barbagialla però può spostarsi solo di una cella verso destra o verso l’alto, cioè ad ogni passo solo una delle sue coordinate può aumentare di una unità.
Trovare il numero N di percorsi diversi disponibili a Barbagialla per raggiungere il tesoro, e il numero massimo MAX e il numero minimo MIN di ghinee d’oro che Barbagialla potrà raccogliere percorrendo questi percorsi.
 14
14
Con il termine: regola (<sigla>,<lista antecedenti>,<conseguente>)
si descrive una regola di inferenza che consente di dedurre o di calcolare il conseguente conoscendo i valori di tutti gli elementi contenuti nella lista degli antecedenti; ogni regola è poi identificata in modo univoco da una sigla.
Per esempio, dato il seguente insieme di regole:
- regola (1, [C1,C2], K)
- regola (2, [K,H], A)
- regola (3, [H,P1], C1)
- regola (4, [H,P2], C2)
- regola (5, [K,A], H)
- regola (6, [P1,P2], H)
- regola (7, [P1,P2], K)
- regola (8, [C1,K], C2)
- regola (9, [C1,C2], A)
si osserva che, conoscendo i valori degli elementi contenuti nella lista [P1,P2], è possibile calcolare (direttamente) H con la regola 6 e K con la regola 7; ma conoscendo [P1,P2] è anche possibile calcolare C1 applicando prima la regola 6 (per calcolare H) e poi la regola 3 (conoscendo ora [H,P1]).
Si può quindi dire che la lista di regole [6,3] rappresenta un procedimento per dedurre o calcolare C1 da [P1,P2]: la lista [6,3] elenca infatti le regole che devono essere via via applicate.
Trovare il numero minimo N di regole che si devono applicare per calcolare A conoscendo [P1,P2].
 15
15
Facendo riferimento alle regole di inferenza descritte nel precedente problema N° 14, trovare i valori di X1, X2 e X3 in modo che la lista di regole [X1, 3, X2, X3] descriva un procedimento per calcolare A a partire da [P1, P2].
 16
16
Dati due gruppi di numeri pari (per esempio: E1 = [4,10,6,8,12] e E2 = [12,14,10,6,10]) e un numero dispari K, (per esempio: K=11) è possibile calcolare il numero N1 di numeri del primo gruppo maggiori di K e il numero N2 di numeri del secondo gruppo minori di K; nell’esempio si ha N1=1, N2=3.
Dati i seguenti due gruppi:
- E1 = [6, 16, 28, 14, 18, 30, 20, 4, 30, 18, 10]
- E2 = [52, 52, 48, 26, 32, 42, 32, 52, 56, 30, 20]
trovare il valore di K che rende minima la somma N1+N2.
 17
17
Mario, Luigi, Piero e Marco giocano con cinque scatole indicate con le prime cinque lettere dell’alfabeto: A, B, C, D, E.
All’inizio del gioco, Mario scrive 4 numeri su 4 foglietti e li inserisce nelle scatole A, B, C e D, uno per scatola. Successivamente Luigi osserva i due foglietti in A e B, copia il valore maggiore su un foglio e lo inserisce nella scatola E. Successivamente, Piero scambia tra loro i foglietti delle scatole B e C, poi quelli delle scatole C e D; infine, Marco scambia i contenuti delle scatole A ed E e quelli delle scatole A e C.
A mo’ di esempio, se Mario ha posto inizialmente 4 in A, 3 in B, 2 in C e 1 in D, la lista risultato (che elenca valori contenuti ordinatamente nelle cinque scatole A, B, C, D, E) risulta L = [1, 2, 4, 3, 4].
Scrivere la lista L dei cinque numeri che si trovano alla fine degli scambi nelle scatole A, B, C, D, E se Mario ha posto inizialmente 7 in A, 8 in B,9 in C e 10 in D.
 18
18
I dieci Cavalieri della Tavola Rotonda (tanti furono in un certo periodo della storia) litigavano spesso per sedersi il più vicino possibile a re Artù.
Per risolvere il problema, decisero di adottare una regola di modifica automatica dei propri posti attorno alla Tavola Rotonda.
A ciascuno dei dieci Cavalieri fu assegnata una delle prime dieci lettere dell’alfabeto (da A a J).
Nella prima riunione, il Cavaliere A era seduto nel posto numero 1, B nel 2, C nel 3 e così di seguito ordinatamente I nel posto 9 e J nel 10.
La lista che descrive le posizioni iniziali è dunque:
- L_PRIMA_RIUNIONE = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Nelle sedute successive, i Cavalieri avrebbero cambiato il proprio posto secondo la regola descritta nella lista di modifica dei posti:
- [(1,7), (2,10), (3,8), (4,5), (5,6), (6,2), (7,9), (8,4), (9,3), (10,1)]
Chi in una riunione occupava il posto indicato dal primo numero di una coppia, nella seduta successiva si sarebbe seduto nel posto indicato dal secondo numero della coppia.
Per esempio: A che nella prima riunione era al posto 1, nella seconda si sarebbe seduto nel posto 7 e nella terza nel posto 9 e poi ordinatamente nei posti 3, 8, 4, 5, 6, 2, 10 per tornare infine al posto 1.
Trovare la lista L_OTTAVA_RIUNIONE che descrive ordinatamente (da A a J) le posizioni dei dieci Cavalieri quando si riuniscono per l’ottava volta.
 19
19
Un treno merci delle Ferrovie Calabro-Lucane con un locomotore e cinque vagoni (denominati VagA VagB, VagC, VagD e VagE) si trova nella configurazione seguente:
- Locomotore VagD VagE VagB VagC VagA
ed è situato nel Binario 1 della zona di manovra rappresentata in figura.
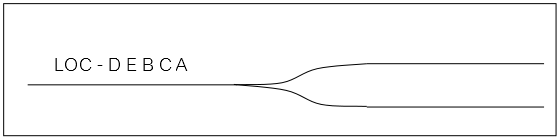
Per effettuare una singola operazione di modifica di configurazione, il locomotore deve spostarsi all’indietro dal Binario 1 al Binario 2 oppure al Binario 3 e successivamente ritornare avanti fino al Binario 1.
La modifica di configurazione consiste nello sganciare tutti o parte dei vagoni agganciati al locomotore una volta arrivato al Binario 2 o al Binario 3, oppure nell’agganciare tutti o parte dei vagoni già presenti sul Binario 2 o sul Binario 3.
Se si vuole riconfigurare il treno perché abbia la seguente configurazione:
- Locomotore VagA VagB VagC VagD VagE
Quale è il numero minimo di operazioni necessarie?
- 3 operazioni
- 5 operazioni
- 7 operazioni
- 9 operazioni
NOTA: per errore la risposta esatta non compare tra quelle proposte…
 20
20
Per descrivere un algoritmo, possiamo utilizzare uno pseudo-linguaggio di programmazione, dove il simbolo ← rappresenta l’istruzione che impone di assegnare al nome simbolico che lo precede il valore calcolato dall’espressione che lo segue
Per esempio: i ← i+1 significa incrementa di 1 il valore associato al nome simbolico i e associa a i il valore incrementato.
Se a i era associato il valore 5, dopo l’esecuzione dell’istruzione a i sarà associato il valore 6.
In questa ipotesi, scegliere la condizione e la istruzione mancanti nel seguente algoritmo in modo che scriva su video il quadrato s di un numero intero n ≥ 0 letto da tastiera:
leggi da tastiera n s ← 0 i ← 0 x ← 1 finché condizione è vera esegui ripetutamente da qui s ← s+x istruzione i ← i+1 a qui scrivi su video s
- condizione: i < n
istruzione: x ← x+2 - condizione: i ≤ n
istruzione: x ← x*2 - condizione: x < n
istruzione: x ← x+2 - condizione: i ≤ n
istruzione: x ← i*2+1