L’algoritmo è noto come metodo babilonese oppure di Archita, di Erone, …
n > 4
Sia n, con n > 4, il numero in ingresso e ![]() la sua radice quadrata allora
la sua radice quadrata allora ![]()
Segui i passi
| Osserva… | |
|---|---|
| Un’approssimazione ragionevole | |
| Un’altra approssimazione ragionevole | |
| Ancora un’approssimazione ragionevole | |
| Ripete il 2° passo | |
| Ripete il 3° passo | |
| … | Continua… |
Riorganizza i passi precedenti
- Considera n=256
- In prima colonna,
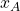 : un’approssimazione della radice che nella prima riga è
: un’approssimazione della radice che nella prima riga è 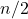 e successivamente sarà il valore in ultima colonna della riga precedente
e successivamente sarà il valore in ultima colonna della riga precedente - In seconda colonna,
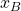 : la divisione tra …
: la divisione tra … - In terza colonna,
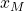 : la media aritmetica tra …
: la media aritmetica tra …
| Passo | |||
|---|---|---|---|
| 1 | 128,00000000 | 2,00000000 | 65,00000000 |
| 2 | 65,00000000 | 3,93846154 | 34,46923077 |
| 3 | 34,46923077 | 7,42691364 | 20,94807220 |
| 4 | 20,94807220 | 12,22069494 | 16,58438357 |
| 5 | 16,58438357 | 15,43620834 | 16,01029596 |
| 6 | 16,01029596 | 15,98971067 | 16,00000331 |
Perché funziona?
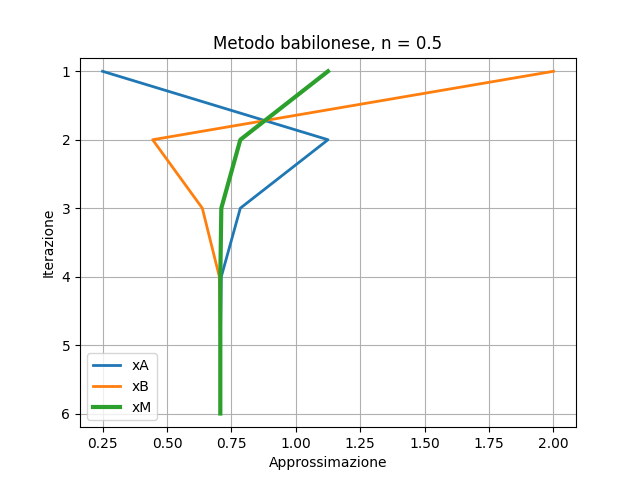
Osserva l’immagine
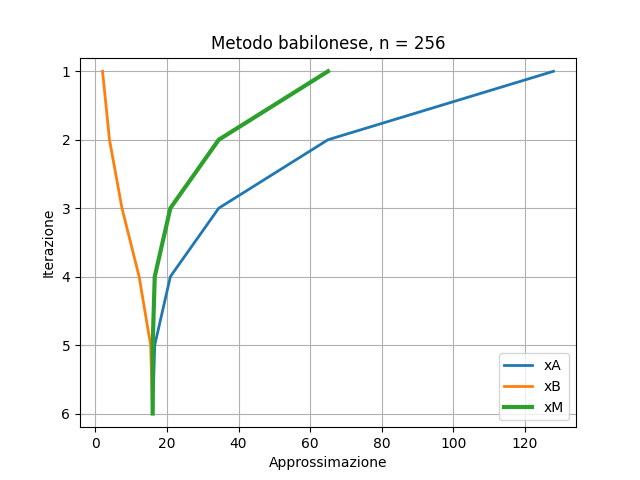
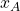 e
e 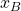 convergono verso
convergono verso 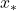
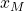 è sempre in mezzo…
è sempre in mezzo…
A ogni iterazione
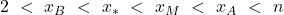
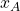 si allontana da n e si avvicina da destra a
si allontana da n e si avvicina da destra a 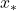
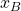 si allontana da 2 e si avvicina da sinistra a
si allontana da 2 e si avvicina da sinistra a 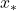
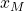 si trova tra
si trova tra 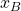 e
e 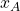
n > 0
L’algoritmo funziona per qualsiasi valore di n (positivo…) e per qualsiasi approssimazione iniziale (positiva…)
A ogni passo
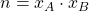
- se
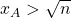 allora
allora 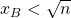
- se
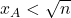 allora
allora 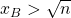
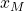 sarà compreso tra
sarà compreso tra 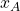 e
e 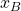 e sempre più vicino a
e sempre più vicino a 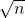
Nei primi 2 passi ![]() e
e ![]() potrebbero scambiarsi di posto ma poi tutto continuerà come prima.
potrebbero scambiarsi di posto ma poi tutto continuerà come prima.
Quante iterazioni?
Per decidere quando fermare l’iterazione si può stabilire un valore soglia ε e fermare l’iterazione quando l’errore è minore di ε
Si può scegliere tra
- Errore assoluto,
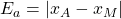 , distanza tra due soluzioni successive
, distanza tra due soluzioni successive - Errore relativo:
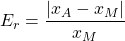 , errore in rapporto all’ultima approssimazione
, errore in rapporto all’ultima approssimazione
Si usa se l’ordine di grandezza dei numeri in gioco è molto alto o molto basso
Esempio
n=256
| Passo | % | |||||
|---|---|---|---|---|---|---|
| 1 | 128,00000000 | 2,00000000 | 65,00000000 | 63,00000000 | 0,96923077 | 96,923077 % |
| 2 | 65,00000000 | 3,93846154 | 34,46923077 | 30,53076923 | 0,88573979 | 88,573979 % |
| 3 | 34,46923077 | 7,42691364 | 20,94807220 | 13,52115857 | 0,64546076 | 64,546076 % |
| 4 | 20,94807220 | 12,22069494 | 16,58438357 | 4,36368863 | 0,26312034 | 26,312034 % |
| 5 | 16,58438357 | 15,43620834 | 16,01029596 | 0,57408762 | 0,03585740 | 3,585740 % |
| 6 | 16,01029596 | 15,98971067 | 16,00000331 | 0,01029265 | 0,00064329 | 0,064329 % |
Le 6 colonne precedenti si possono ridurre a 2!
- L’approssimazione occupa una sola colonna
- Scegli il criterio per fermare l’iterazione (per esempio errore assoluto)
| Approssimazione | Errore assoluto | |
|---|---|---|
| 128,00000000 | ||
| 65,00000000 | 63,00000000 | |
| 34,46923077 | 30,53076923 | |
| 20,94807220 | 13,52115857 | |
| 16,58438357 | 4,36368863 | |
| 16,01029596 | 0,57408762 | |
| … | … | … |
| … | … |
Wikipedia: Metodi per il calcolo della radice quadrata