Emma fa questo gioco: lancia un dado con facce numerate da 1 a 6; se esce il numero 3 guadagna 3 punti, altrimenti perde 1 punto.
Il punteggio iniziale è 0.
- Qual è la probabilità che, dopo 4 lanci, il suo punteggio sia ancora 0?
- Qual è la probabilità che, in una sequenza di 6 lanci, il punteggio non scenda mai sotto lo 0?
1. Qual è la probabilità che, dopo 4 lanci, il suo punteggio sia ancora 0?
- Calcolo del punteggio al variare del numero di volte che esce 3
- n=0, punteggio=-4
- n=1, punteggio=0
- n=2, punteggio=4
- n=3, punteggio=8
- n=4, punteggio=12
- Il punteggio rimane 0 dopo 4 lanci se il 3 esce 1 volta
- p(punteggio = 0) = p(n = 1) = …
- p(dado = 3) = 1/6
- p(dado = x) = 5/6, x <> 3
- p(dado = 3xxx) =
- p(dado = x3xx) =
- p(dado = xx3x) =
- p(dado = xxx3) =
- p(n = 1) =
=
=
∼ 0.3858 = 38,58 %
2. Qual è la probabilità che, in una sequenza di 6 lanci, il punteggio non scenda mai sotto lo 0?
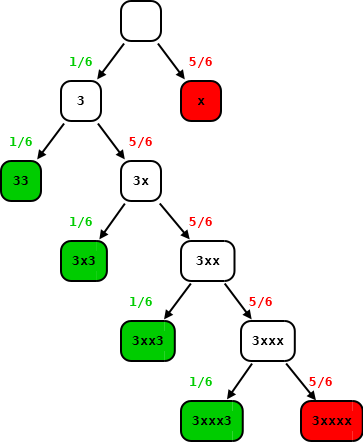 Sia * qualsiasi uscita da 1 a 6
Sia * qualsiasi uscita da 1 a 6
Considera i casi con punteggio positivo o nullo (in verde)
- p(dado = 33****) =
- p(dado = 3×3***) =
- p(dado = 3xx3**) =
- p(dado = 3xxx3*) =
p(punteggio ≥ 0) = +
+
+
~ 0,08629 ~ 8,63 %
Oppure, considera i casi con punteggio negativo (in rosso)
- Se al primo lancio esce un numero diverso da 3 il punteggio è già negativo!
- p(dado = x*****) =
- p(dado = x*****) =
- Se al primo lancio esce 3 e poi escono 4 numeri diversi da 3 il punteggio diventa negativo al 5° lancio
- p(dado = 3xxxx*) =
- p(dado = 3xxxx*) =
- In nessun altro caso il punteggio sarà negativo
p(punteggio ≥ 0) = 1 – –
~ 0,08629 ~ 8,63 %
Esercizi aggiuntivi…
2. Qual è la probabilità che, in una sequenza di 6 lanci, il punteggio non scenda mai sotto lo 0?
Con controllo alla fine dei 6 lanci.
- Calcolo del punteggio al variare del numero di volte che esce 3
- n=0, punteggio=-6
- n=1, punteggio= -2
- n=2, punteggio=2
- n=3, punteggio=6
- n=4, punteggio=10
- n=5, punteggio=14
- n=6, punteggio=18
- Il punteggio non scende sotto lo 0 se il 3 esce almeno 2 volte
- p(punteggio ≥ 0) = p(n ≥ 2) = 1 – p(n < 2) = 1 – p(n = 0) – p(n = 1) = …
- p(n = 0) = p(dado = xxxxxx) =
=
- p(n = 1) =…
- p(dado = 3xxxxx) = … =
- p(dado = x3xxxx) = …
- p(dado = xx3xxx) = …
- p(dado = xxx3xx) = …
- p(dado = xxxx3x) = …
- p(dado = xxxxx3) = …
- p(dado = 3xxxxx) = … =
- p(punteggio ≥ 0) =
=
= … ∼ 0,2632 = 26,32 %
- p(n = 0) = p(dado = xxxxxx) =
Calcola la probabilità di ogni punteggio dopo 4 lanci
| Numero di 3 |
punti | uscite | quante sono |
probabilità | probabilità (distribuzione binomiale) |
| 0 | -4 | xxxx | |||
| 1 | 0 | 3xxx – x3xx – xx3x – xxx3 | |||
| 2 | 4 | 33xx – 3x3x – 3xx3 – x33x – x3x3 – xx33 | |||
| 3 | 8 | 333x – 33×3 – 3×33 – x333 | |||
| 4 | 12 | 3333 |
Calcola la probabilità di ogni punteggio dopo 6 lanci
| Numero di 3 |
punti | uscite | quante sono |
probabilità | probabilità (distribuzione binomiale) |
| 0 | -6 | xxxxxx | |||
| 1 | -2 | 3xxxxx – x3xxxx – xx3xxx – xxx3xx – xxxx3x – xxxxx3 | |||
| 2 | 2 | 33xxxx – 3x3xxx – 3xx3xx – 3xxx3x – 3xxxx3 – x33xxx x3x3xx – x3xx3x – x3xxx3 – xx33xx – xx3x3x – xx3xx3 xxx33x – xxx3x3 – xxxx33 |
|||
| 3 | 6 | 333xxx – 33x3xx – 33xx3x – 33xxx3 – 3x33xx – 3x3x3x 3x3xx3 – 3xx33x – 3xx3x3 – 3xxx33 – x333xx – x33x3x x33xx3 – x3x33x – x3x3x3 – x3xx33 – xx333x – xx33x3 xx3x33 – xxx333 |
|||
| 4 | 10 | 3333xx – 333x3x – 333xx3 – 33x33x – 33x3x3 – 33xx33 3x333x – 3x33x3 – 3x3x33 – 3xx333 – x3333x – x333x3 x33x33 – x3x333 – xx3333 |
|||
| 5 | 14 | 33333x – 3333×3 – 333×33 – 33×333 – 3×3333 – x33333 | |||
| 6 | 18 | 333333 |
Calcola la probabilità delle uscite significative con 6 lanci
| Uscite | quante sono |
probabilità | |
| 33**** | |||
| 3×3*** | |||
| 3xx3** | |||
| 3xxx3* | |||
| 3xxxx* | |||
| x***** | |||