Esame di Stato 2017 – 9

2024-05-052018-03-31 di admin

Dimostrare che l’equazione $\arctan x +x^3+e^x = 0$ ha una e una sola soluzione reale.

Sia $f(x) = \arctan x +x^3+e^x$

Esistenza

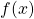$f(x)$ è continua in R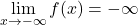
$\displaystyle \lim_{x\to-\infty}f(x)=-\infty$
$\displaystyle \lim_{x\to+\infty}f(x)=+\infty$
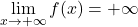
Teorema degli zeri: esiste almeno uno zero…

Unicità

$f'(x)=\frac{1}{1+x^2}+3x^2+e^x$
$f\prime(x) > 0$
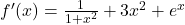
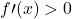
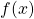$f(x)$ crescente in R
No punti notevoli
Un solo zero

Approssimazione

$f(0)=1 > 0$
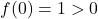
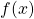$f(x)$ crescente in R: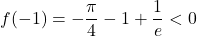 $\displaystyle f(-1)=-\frac{\pi}{4}-1+\frac{1}{e} < 0$
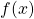$f(x)$ ha segni discordi in [-1, 0]
Esiste x0 in (-1, 0) tale che f(x0) = 0

Conclusione

L’equazione $\arctan x +x^3+e^x = 0$ ha una e una sola radice reale in (-1, 0).