Livia per andare a scuola usa l’autobus e può utilizzare la linea 1 o la linea 2.
Quando arriva alla fermata sotto casa, la probabilità che il primo autobus che passi sia della linea 1 è 0,6.
La probabilità di trovare posto a sedere sulla linea 1 è 0,2, mentre sulla linea 2 è 0,5.
Questa mattina Livia ha preso il primo autobus che è passato ed è riuscita a sedersi.
Qual è la probabilità che sia arrivata con la linea 1?
Osserva la figura
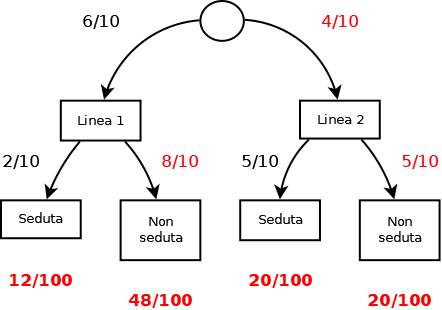
Fai tutti i calcoli
| p(L1) | = | |
| p(S | L1) | = | |
| p(S e L1) | = p(L1) · p(S | L1) | |
| = | ||
| p(L2) | = 1 – p(L1) | |
| = | ||
| p(S | L2) | = | |
| p(S e L2) | = p(L2) · p(S | L2) | |
| = | ||
| p(S) | = p(S e L1 oppure S e L2) = p(L1) · p(S | L1) + p(L2) · p(S | L2) | |
| = | Livia arriva seduta 32 volte su 100 | |
| p(L1 | S) | = = | |
| = | Se Livia arriva seduta allora 3 volte su 8 è con la linea 1 |
