Considera un cerchio di raggio unitario con centro nell’origine.
Sapendo che l’area di uno dei 4 settori circolari è ![]() calcola un valore approssimato di pi greco utilizzando uno dei metodi di integrazione di tipo geometrico.
calcola un valore approssimato di pi greco utilizzando uno dei metodi di integrazione di tipo geometrico.
Metodo delle parabole
| Parabole | n | h | Area | = | ||
|---|---|---|---|---|---|---|
| 1 | 2 | = 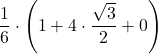 | ||||
| = | ||||||
| Pi greco | = | |||||
= 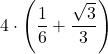 | ||||||
| = | ||||||
| = 2,976… | ||||||
| Parabole | n | h | Area | = | ||
| 2 | 4 | = 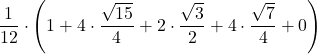 | ||||
| = | ||||||
| Pi greco | = | |||||
= 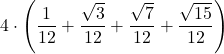 | ||||||
| = | ||||||
| = 3,08… |