Una moneta di 1 euro (il suo diametro è di 23,25 mm) viene lanciata su un pavimento ricoperto con mattonelle esagonali (regolari) di lato 10 cm.
Qual è la probabilità che la moneta vada a finire internamente a una mattonella (cioè non tagli i lati degli esagoni)?
Vedi 2009 PNI – 3
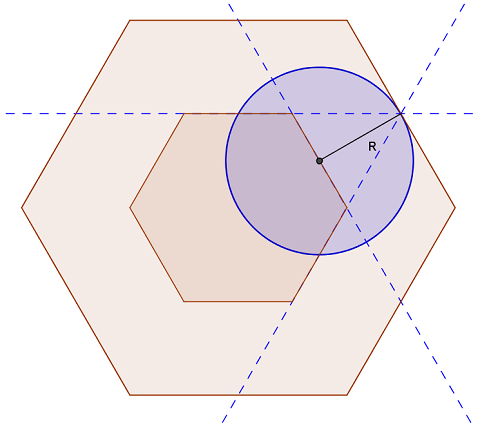 La moneta non tocca il bordo se il suo centro cade a una distanza dai bordi maggiore del suo raggio, cioè se cade all’interno dell’esagono interno
La moneta non tocca il bordo se il suo centro cade a una distanza dai bordi maggiore del suo raggio, cioè se cade all’interno dell’esagono interno
Siano
- L: lato della piastrella
- S: superficie della piastrella
- D: diametro della moneta
- A: apotema, altezza del triangolo equilatero di lato L
- Ai: apotema dell’esagono interno
- Si: superficie dell’esagono interno
- pi: probabilità che la moneta cada all’interno
La probabilità che la moneta cada all’interno è data dal rapporto tra la superficie dell’esagono interno Si e della piastrella intera S
- L = 10 cm
- D = 2R = 23,25 mm = 2,325 cm
- A =
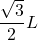
- Ai = A – R
- pi =
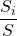
Osserva
- Il rapporto tra le superfici dei due esagoni è uguale al rapporto tra i quadrati dei lati
- Il rapporto tra le superfici dei due esagoni è uguale al rapporto tra i quadrati degli apotemi
Calcoli…
![]() ~ 75%
~ 75%
Se vuoi dimostrare che…
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= 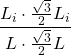 =
= ![]()
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= 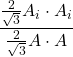 =
= ![]()
![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]()