Questo gioco è stato inventato da Sam Loyd, il grande esperto in giochi matematici americano, ed era, un tempo, molto popolare nelle fiere e feste di paese.
Sul tavolo da gioco ci sono sei quadrati segnati con i numeri 1, 2, 3, 4, 5, 6. I giocatori devono mettere la loro posta in uno dei sei quadrati e successivamente vengono lanciati tre dadi.
- Se il numero scelto compare soltanto su un dado il giocatore riceve indietro il suo denaro e in più la stessa somma.
- Se compare su due dadi, riceve indietro il suo denaro più il doppio della stessa somma.
- Se compare su tutti e tre i dadi riceve indietro il suo denaro più il triplo della stessa somma.
- Ovviamente se il numero scelto dal giocatore non compare su nessuno dei tre dadi, chi tiene il banco ritira la somma giocata.
Chiariamo il gioco con un esempio.
- Supponiamo che il giocatore punti un Euro sul 6.
- Se esce il 6 su uno dei tre dadi, il giocatore riceve indietro il suo Euro, più un altro Euro.
- Se il 6 esce su due dadi, riceve indietro il suo Euro, più altri due Euro.
- Nel caso in cui esca il 6 su tutti e tre i dadi, il giocatore riceve indietro il suo Euro, più altri tre Euro.
Il giocatore potrebbe fare questo ragionamento: se la probabilità che esca il mio numero su un dado è 1/6, allora su tre dadi sarà il triplo, cioè 3/6 ovvero 1/2, quindi il gioco è onesto e posso giocare tranquillamente. Ma è corretto questo ragionamento? E se non lo è, qual è la probabilità di vincere o di perdere al gioco?
Il giocatore punta sull’uscita del numero x e lancia i 3 dadi
- p(x esce 0 volte) =
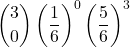 =
= 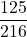
- p(x esce 1 volta) =
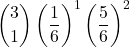 =
= 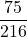
- p(x esce 2 volte) =
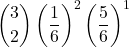 =
= 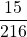
- p(x esce 3 volte) =
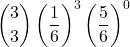 =
= 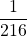
Speranza matematica
![]()
= ![]()
= ![]() = -0,0787… ~ -7,87… %
= -0,0787… ~ -7,87… %